TR3.5

Combining Resistors Method

Houjun Liu 2021-09-27 Mon 12:00

1 Combining Resistors Method

The KBhPHYS201KirkoffsLaws Kirkoff's Laws themselves often requiring solving >6x6 matrixes to solve equations quickly. Which is hard.

1.1 Series

If you have two resisters…

–—|||–—|||–—

With the first having a resistance of \(A\Omega\) and the second \(B\Omega\).

The total resistance would simply be \((A+B)\Omega\).

  • Same as equivalent of "electricity!" go through the first then the second

#disorganized

1.2 Parallel

Smaller area |–—|||-–— | Bigger area |===|||====

\(R_2 = R_1 \times \frac{A_1}{A_2}\)

\(R_{eq} = R_1 \times \frac{A_1}{A_1+A_2}\)

\(\frac{1}{R_{eq}} = \frac{A_1+A_2}{A_1R_1}\)

\(\frac{1}{R_{eq}} = \frac{1}{R_1} + \frac{A_2}{A_1R_1}\)

\(\frac{1}{R_{eq}} = \frac{1}{R_1} + \frac{1}{R2}\)

Resistance equation for series :pointup:

#disorganized

Calculate resistsance

1.3 "Combine Resistors" Method

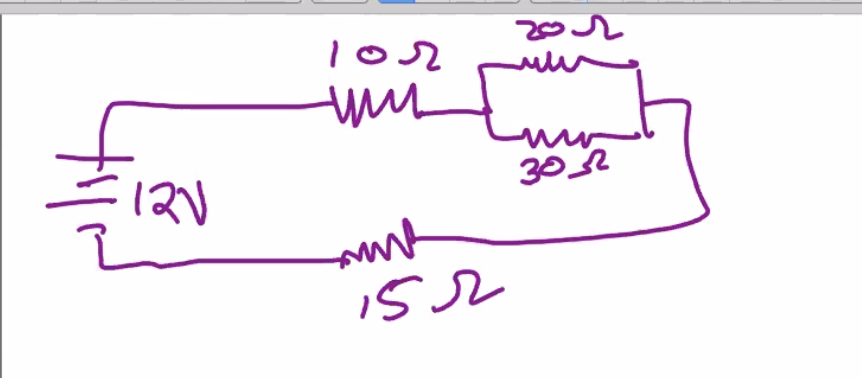
Screen Shot 2020-09-14 at 11.02.45 AM.png

Figure 1: Screen Shot 2020-09-14 at 11.02.45 AM.png

1.3.1 Parallel Resistors as Single Resistors

Per the previous resisters rules, that \(\frac{1}{R_{eq}} = \frac{1}{R_1} + \frac{1}{R2}\), we could treat the \(20 \Omega\) and \(30 \Omega\) in parallel as a single resistor of \(12 \Omega\).

Now the circut becomes even simpler:

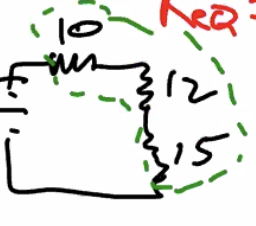
Screen Shot 2020-09-14 at 11.05.49 AM.png

Figure 2: Screen Shot 2020-09-14 at 11.05.49 AM.png

1.3.2 Sequence Resistors as Single Resistors

Per the sequence resisters rules, that total resistance is \((A+B)\Omega\), we could combine these three resistors as a \(37 \Omega\) resistor.

1.3.3 Combined Current

We know that \(12V / 37\Omega = 0.324 Amps\) is the current that returns to the battery and what the battery starts with, for if we treat the circuit as a single resistor, the 12 volts would only be working against.

From there, once we have a current for beginning and end, we could work our way up backwards by calculating the final voltage.

  • Multiples battries can't be solved with the combined resistor method
  • So, first guess the current flow
    • Each batteries' current will flow back to itself
    • When currents meet, they will combine
  • Use currents identified before + Kirkoff's second law
  • Use Kirkoff's first law to find loops (and hence equations) that, together, covers all components
  • If resulting currents is negative, that means that you drew the current in the wrong direction, or you are charging a battery
    • Either way, if the signs are preserved to solve the rest of the equation, you should be fine numerically
    • Just update your graph to reflect the actual currents' directions

LED longer leg is positive