Backlinks
#ref
1 Capacitors vs. Batteries
Batteries => Converting \(PE_{chem}\) => Eletrical energy
Capacitors => Converting \(PE_{elec}\) => Eletrical energy
When you are discharging a battery, they remain at constant voltage until they are used up, at which point the voltage drop like a plate.
When you are discharging a capacitor, there is a linear fall in voltage that is constant.
Charge remaining: capacitance times voltage
2 Energy on a Capacitor
A little bit #disorganized
Energy stored on a capacitor: \(E=\frac{V_c * Q}{2}\).
Charge on a capacitor: \(Q = C \times V_c\)
Farads: \(F = \frac{C}{V}\)
So, putting this together, the energy stored on a capacitor would be…
\definition[as $Q=C \times V_c$]{Energy stored in a capacitor}{\(E=\frac{V \times Q}{2} = \frac{CV^2}{2}\)} \(Q_{cap} \propto V\). In fact \(Q_{cap} = C \times V_c\).
3 Capacitors interacting with Resistance
As you increase the KBhPHYS201ResistanceConductivity, the a capacitor of the same capacitance would charge slower. ("Less charge flows in")
As you fix the Resistance, the capacitor of a higher capacitance would charge slower. ("Need more change to fill")
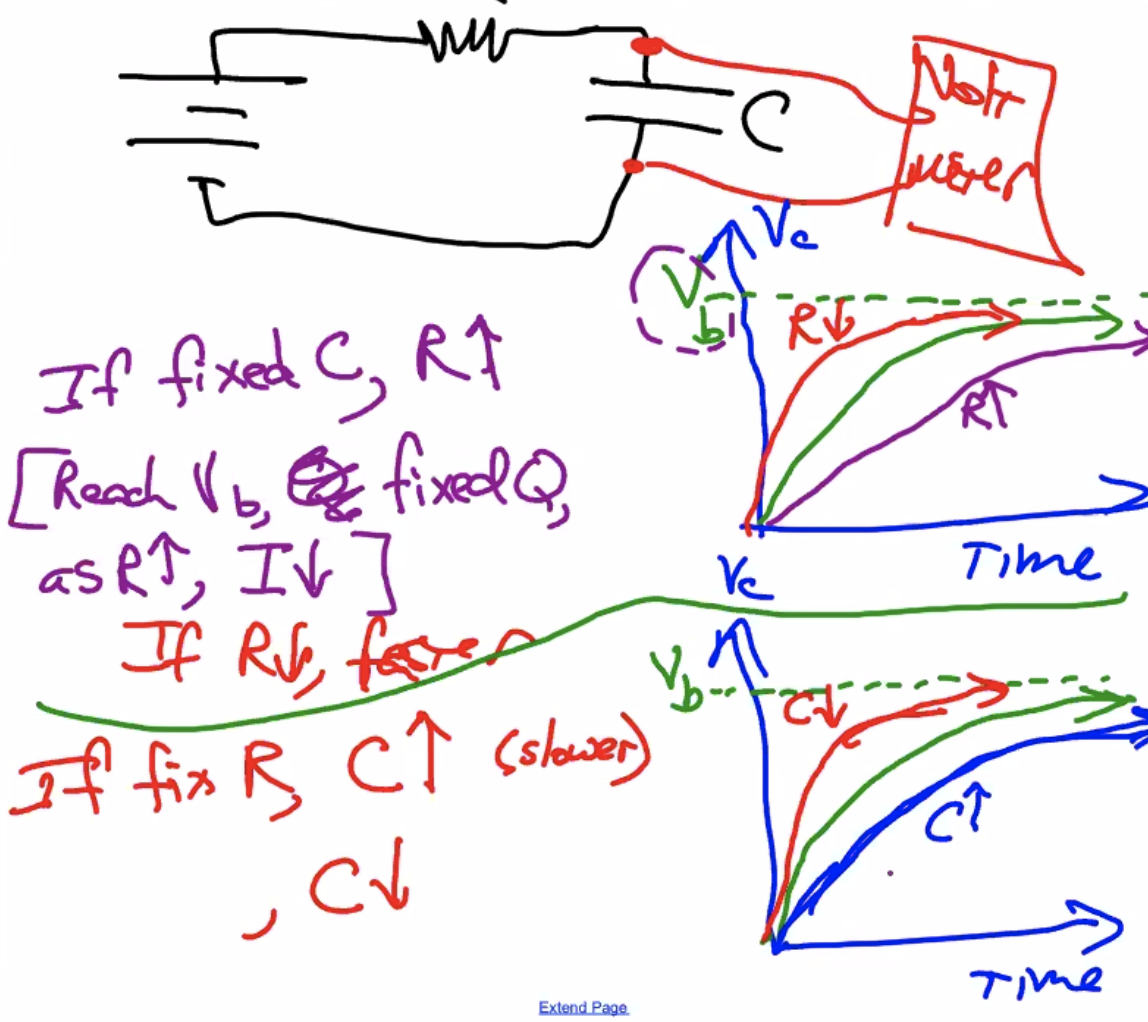
Figure 1: Screen Shot 2020-09-30 at 10.42.44 AM.png
Charging time is in fairly good agreement with resistance times capacitance.
So… #disorganized
Experimentally, "Charging time", \(\tau\) \(\approx R \times C\).
Let's check the units!
- \(V = IR\)
- \(R = \frac{V}{I}\)
- So \(R = \omega = \frac{V * s}{Q}\)
- \(Q = CV\)
- So \(\frac{Q}{V} = C\)
Hence, \(R \times C = \frac{\cancel{V} \times s}{\cancel{Q}} = \cancel{\frac{Q}{V}}\), indeed, has a unit Seconds!
4 Equations modeling charging a capacitor
\definition[where $R$ is the resistance, $C$ is the capacitance]{Time Constant Tau}{$RC = \tau$ — time constant to be able to change the capacitor to a useful voltage; aka how much does the capacitor need to noticeably charge/discharge.} Now that we have this value, we could also represent the full charge process using the equations as follows:
\definition[where $V_b$ is the battery voltage, $t$ is time elapsed, $R$ is resistance, and $C$ is the capacitance]{Current in circuit as you charge a capacitor}{\(I(t) = \frac{V_b}{R} \times e^{\frac{-t}{RC}}\)} As you start to charge a capacitor, the current starts at \(\frac{V_b}{R}\) — current just without the resistor. Then, it will slowly drop down to 0.
\definition[where $V_b$ is the battery voltage, $t$ is time elapsed, $R$ is resistance, and $C$ is the capacitance]{Voltage before and after a capacitor as you charge a capacitor}{\(V(t) = V_b \times (1 - e^{\frac{-t}{RC}})\)} #disorganized
5 Capacitors in series and parallel
Helpful to see: KBhPHYS201CombiningResistors
5.1 Capacitors in Parallel
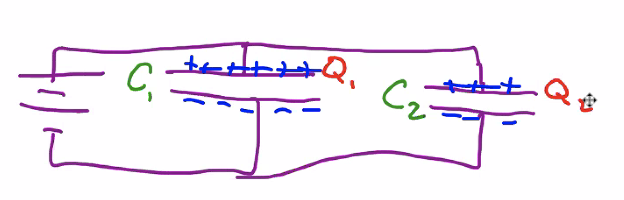
Figure 2: Screen Shot 2020-10-07 at 10.20.06 AM.png
\(Q_{tot} = Q_1 + Q_2\).
And, because of the fact that \(C = \frac{Q}{V}\), \(V\times C_{eq} = V \times C_1 + V \times C_2\)
Dividing \(V\) out of the previous equations \(C_{eq} = C_1 + C_2\).
Capacitors in parallel act like resistors in series.
5.2 Capacitors in Series

Figure 3: Screen Shot 2020-10-07 at 10.23.08 AM.png
Because of the fact that the middle wire does not carry any changes, it is "neutral" and simply polarized — making \(Q_1\) equaling \(Q_2.\)
Why is this? If the middle bit is neutral, the \(Q^+\) on one end would equal to the \(Q^-\) on the other. Correspondingly, the other side of the plates of the capacitor would have the opposite of the same values \(Q^-\) and \(Q^+\) on the neutral middle plate.
By the transitive property, \(Q_1 = Q_2\).
Because \(V_1 + V_2 = V_b\) — see KBhPHYS201CombiningResistors & \(C = \frac{Q}{V}\) , \(\frac{Q_1}{V} + \frac{Q_2}{V} = \frac{Q_{tot}}{V}\).
Given \(Q_1 = Q_2\).
So
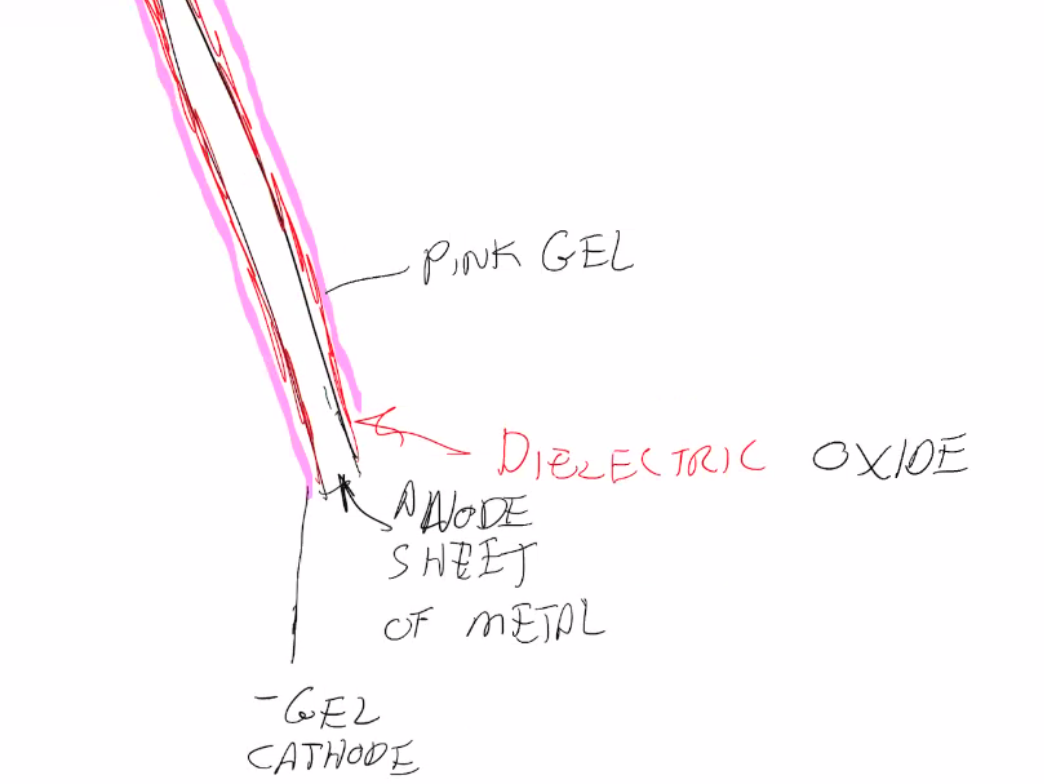
5.3 Construction of Capacitors
A diagram of the plates inside a polar capacitor before being rolled up.