Table of Contents
1 Resistance
So, let's figure out resistance.
We know that… \(V\) = \(\frac{J}{C}\), per KBhPHYS201Voltage, and we also know that resistance would equal a unit \(\frac{Vs}{c}\) given that \(I = \frac{C}{s} = \frac{\Delta V}{Resistance}\) (see KBhPHYS201Current Current). Plugging in the definition of voltage, we get that resistance is measured in \(\frac{Js}{C^2}\). We call this unit Ohms, or \(\Omega\).
\definition{Resistance $\Omega$}{A value measured in \(\frac{Js}{C^2}\) that measures the resistance to current}
1.0.1 Calculating resistance
- So, let's think. With a wire of length L and with a wire of area A, if we increase L, the resistance in the wire would increase; if we increase area A, the resistance in the the wire would decrease.
- \(Resistance = \frac{L}{A}*ResistivityOfMaterial\) with units \(\frac{m}{m^2}(\Omega \times m)\).
Sometimes its easier to think about conductivity.
and, indeed, resistivity of materials are measured in \(\Omega \times m\), which also makes sense intuitively.
1.0.2 Heat of resistance
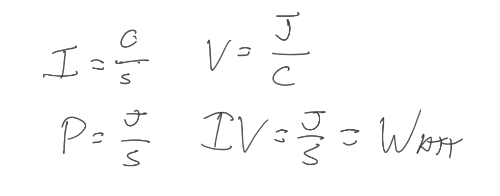
Figure 1: KBe20phys250srcHeatFromResistors.png
2 Ohm
\[\Omega = \dfrac{\text{V}}{\text{A}} = \dfrac{1}{\text{S}} = \dfrac{\text{W}}{\text{A}^2} = \dfrac{\text{V}^2}{\text{W}} = \dfrac{\text{s}}{\text{F}} = \dfrac{\text{H}}{\text{s}} = \dfrac{\text{J} {\cdot} \text{s}}{\text{C}^2} = \dfrac{\text{kg} {\cdot} \text{m}^2}{\text{s} {\cdot} \text{C}^2} = \dfrac{\text{J}}{\text{s} {\cdot} \text{A}^2}=\dfrac{\text{kg}{\cdot}\text{m}^2}{\text{s}^3 {\cdot} \text{A}^2}\] (Wikipedia)