1 Kirkoff's Laws
1.1 Kirkoff's First Law
\definition{Kirkoff's First Law}{**Sum of voltage in any closed loop should add up to 0**} As in, the sum of all voltage changes from Start => Start will add up to 0.
1.2 Kirkoff's Second law
\definition{Kirkoff's Second Law}{**Net current flowing into a node is 0**} With a current \(i_0\), when it flows into a junction like B, the current \(i_0\) splits into \(i_2\) and \(i_3\)
1.3 A Quick Kirkoff Excercise
Here's a circuit:
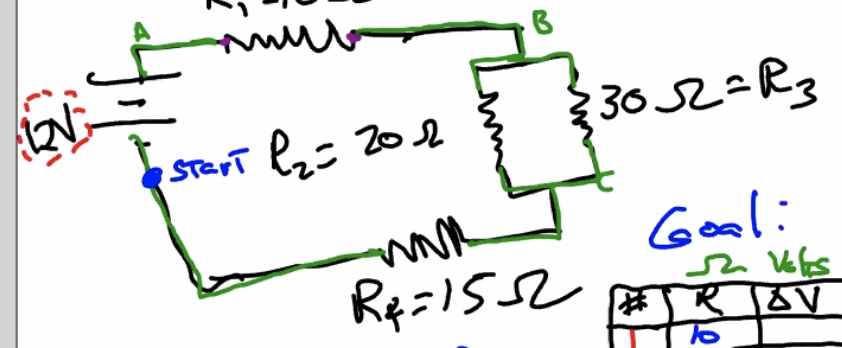
Figure 1: Screen Shot 2020-09-14 at 10.38.44 AM.png
So, to calculate the resistance and current at every point o
START at start
- \(+12\)
- \(-I_1*10\) (per \(I = \frac{\Delta V}{resistance}\))
- \(-I_2 * 20\)
- \(-I_1 * 15\)
- \(= 0\)
\(I_1 - I_2 - I_3 = 0\), per Kirerbab's Second Law.