Backlinks
1 Limits
1.1 Warming up
Here's a function
\(y = \frac{1}{x}\).
We know that it has
- Domain \(D (-\infty, 0)(0, \infty)\)
- Range \(R (-\infty, 0)(0, \infty)\)
- \(As\ x\to\infty,\ y\to0\)
- Function is odd, that is, \(f(-x) = -f(x)\)
1.2 The Limit Notation
1.3 Computing Limits Algebraically
1.4 Types of Discontinuity
1.5 Error and Epsilon Delta Proofs
1.6 CN10062020 Continuity
#disorganized #flo
\(\lim_{x \to a} f(x) \neq f(a)\).
Sometimes
*A function is continuous at \(x=a\) if ALL OF the following three conditions:$
- \(\lim_{x\to a} f(x)\) exists
- \(f(a)\) exists
- \(\lim_{x\to a} f(x) = f(a)\)
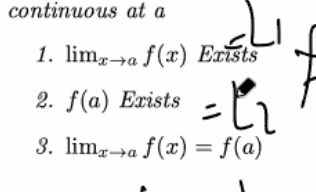
Figure 1: threestepslimit.png
\definition{Removable discontinuity}{Removeable discontinuity are often holes. They are discontinuities that, with an additional definition, one could remove.} For instance, \(f(x) = \frac{x^2-x-2}{x-2}\) has a hole at \(x=2\), but if we defined a value for \(x=2\), our lovely discontinuity is immediately removed.
\defintion{Infitinite discontinuity}{Functions that approch infinity} If you think about it, if you try to fix the discontinuity, you will be tracing all the way up the infinity
\definition{Jump discontinuity}{"Staircase" functions that causes jump} Like…
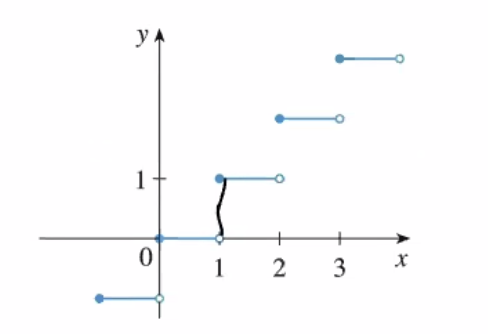
Figure 2: jumpdisc.png
As you could see, if you try to fix the discontinuity, this would result in vertical lines, which is illegal in functions.
Continuous-from-right: \(f(a) = \lim{x \to a^+} f(x)\) Continuous-from-left: \(f(a) = \lim{x \to a^-} f(x)\)