Backlinks
Table of Contents
1 Derivatives
=> Instantaneous rate of change at a particular point
- Average rate of change = \(\frac{\Delta Y}{\Delta X}\)
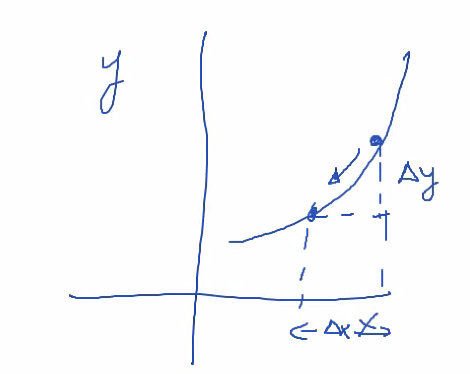
Figure 1: rateofchange.png
- Instantaneous rate of change = \(\lim_{\Delta x \to 0} \frac{\Delta Y}{\Delta X}\)
Derivative of \(f(x)\) => \(\frac{dy}{dx}\)
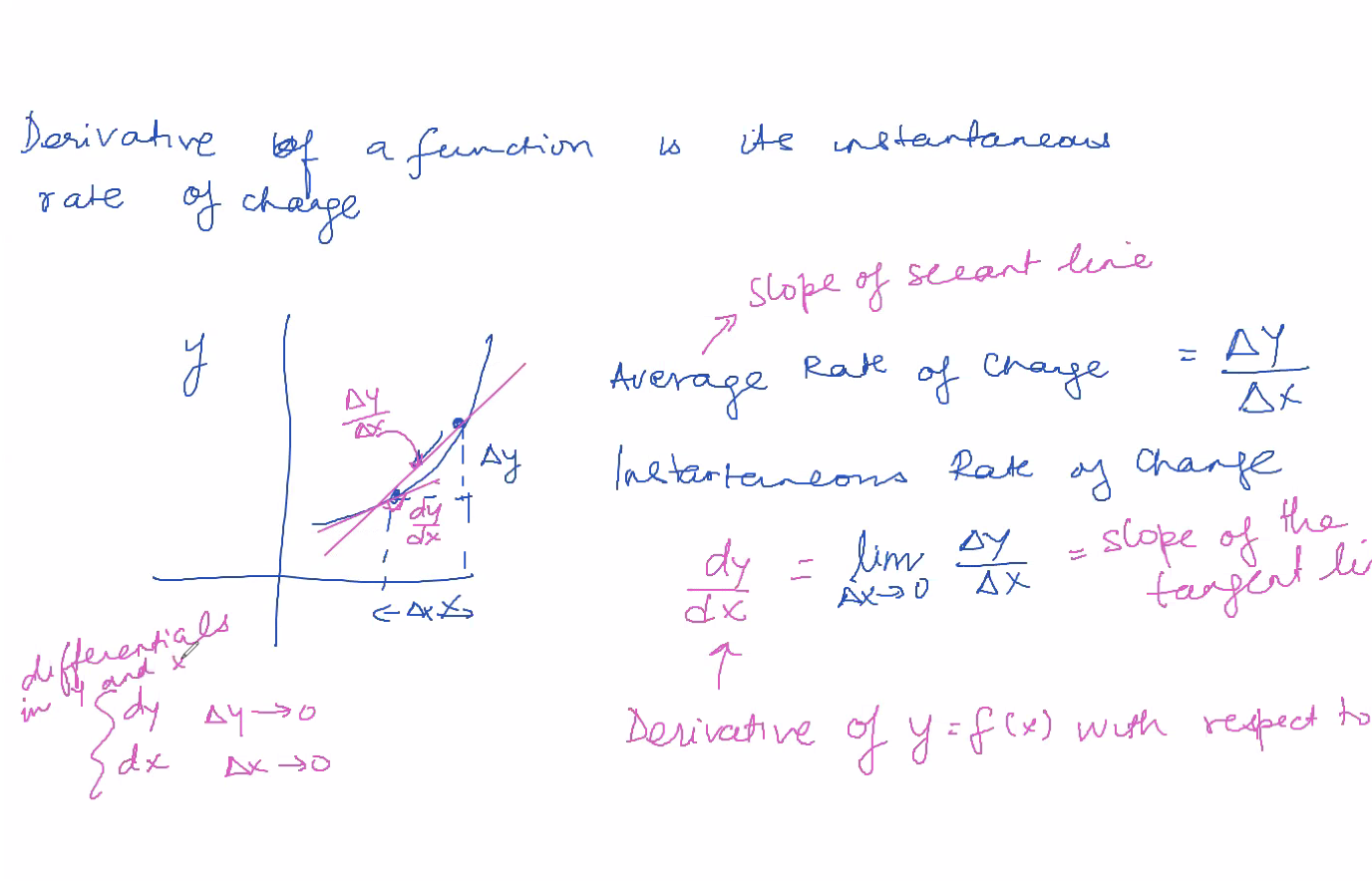
Figure 2: derivativesWB.png
1.1 Useful Table of Derivatives
| f(x) | f'(x) |
|---|---|
| \(x^2\) | \(2x\) |
| \(x^3\) | \(3x^2\) |
| \(x^n\) | \(nx^{n-1}\) |
| \(\frac{1}{x}\) | \(\frac{-1}{x^2}\) |
| \(\sqrt{x}\) | \(\frac{1}{2 \sqrt{x}}\) |
| \(\sin(x)\) | \(\cos (x)\) |
| \(\cos(x)\) | \(-\sin (x)\) |
| \(\tan(x)\) | \(1 + \tan^2 (x) = sec^2(x)\) |
| \(\cot(x)\) | \(-\csc^2 (x)\) |
| \(\sec(x)\) | \(\tan(x) \sec(x)\) |
| \(\csc(x)\) | \(-\cot(x) \csc(x)\) |
| \(e^x\) | \(e^x\) |
| \(ln(x)\) | \(\frac{1}{x}\) |
| \(a^x\) | \(a^x ln(a)\) |
| \(log_a(x)\) | \(\frac{1}{x ln(a)}\) |
| \(f^-1(x)\) | \(\frac{1}{f'(f^-1(x))}\) |
| \(sin^-1(ax)\) | \(\frac{a}{\sqrt{1-(ax)^2}}\) |
| \(cos^-1(ax)\) | \(\frac{-1}{\sqrt{1-(ax)^2}}\) |
| \(tan^-1(ax)\) | \(\frac{1}{1+(ax)^2}\) |