Backlinks
- lrm;
Table of Contents
1 Problems on slide 38
1.1 Problem 36
\[
\begin{aligned} \lim_{x\to 0}\sqrt{x^3+x^2} sin\frac{\pi}{x}=0 \\& -1 \le sin\frac{\pi}{x} \le 1 \\&\therefore -\left| x \sqrt{x+1} \right| \le x \sqrt{x+1} sin \frac{\pi}{x}\lt \left| x \sqrt{x+1}\right| \end{aligned}\]
\begin{aligned} \lim_{x\to 0} -\left|x\sqrt{x+1}\right| = -\left|0\sqrt{1}\right| = 0\\ \lim_{x\to 0} \left|x\sqrt{x+1}\right| = -\left|0\sqrt{1}\right| = 0\\ \therefore \lim_{x\to 0} = \sqrt{x^3+x^2}\sin\frac{\pi}{x} = \boxed{0} \end{aligned}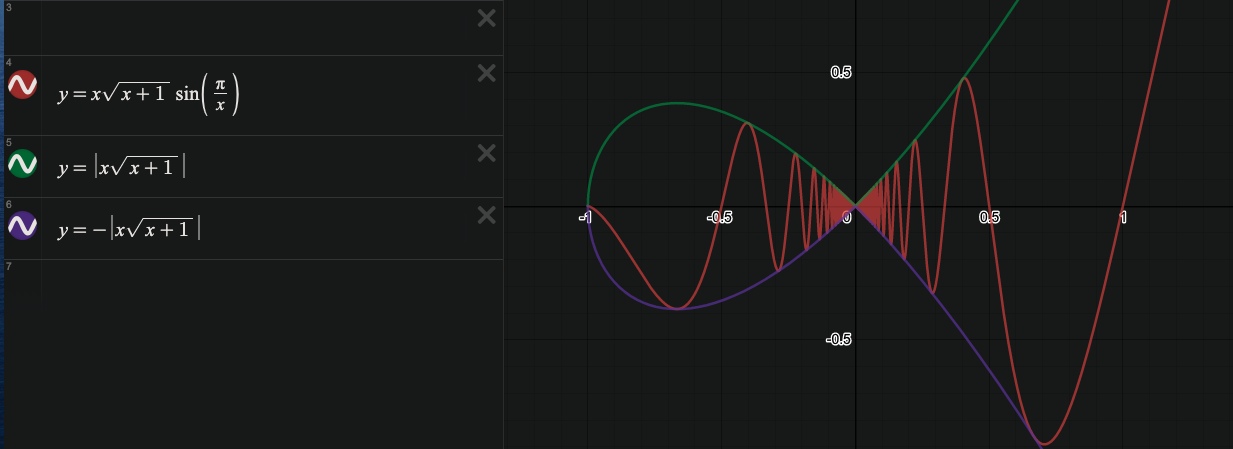 \[
\[
\]
1.2 Problem 37
\[
\begin{aligned} \lim_{x\to 4}4x-9 = 4(4)-9 = 16-9 = 7\\ \lim_{x\to 4}x^2-4x+7 = 4^2 - 4(4) + 7 = 7\\ 4x-9 \le f(x) \le x^2 - 4x+7\\ \therefore \lim_{x\to 4}f(x) = \boxed{7} \end{aligned}\]
1.3 Problem 38
\[
\begin{aligned} \lim_{x\to 1}2x = 2(1) = 2\\ \lim_{x\to 1}x^4-x^2+2 = 1 - 1 + 2 = 2\\ 2x \le g(x) \le x^2 - x^2 + 2\\ \therefore \lim_{x\to 1}g(x) = \boxed{2} \end{aligned}\]
1.4 Problem 39
This one is doable by just saying that \(\lim\limits_{x\to 0}x^4cos\frac{2}{x} = \lim\limits_{x\to 0} x^4 \lim\limits_{x\to 0}cos\frac{2}{x} = 0\left(\lim\limits_{x\to 0} cos\frac{2}{x}\right) = 0\).
But we can also do it properly: \[
\begin{aligned} -1 \le cos\frac{2}{x}\le 1\\ \therefore -x^4 \le x^4 cos\frac{2}{x} \le x^4\\ \lim_{x\to 0} -x^4 = 0 = \lim_{x\to 0} x^4 \\ \therefore \lim_{x\to 0}x^4cos\frac{2}{x} = \boxed{0} \end{aligned}\]
1.5 Problem 40
- inspired by GUESS GOD
So originally you notice that \(\sqrt{0}\) is just \(0\) so the thing is going to be zero in the end either way
But we can guess god our way to the nice functions using this graph
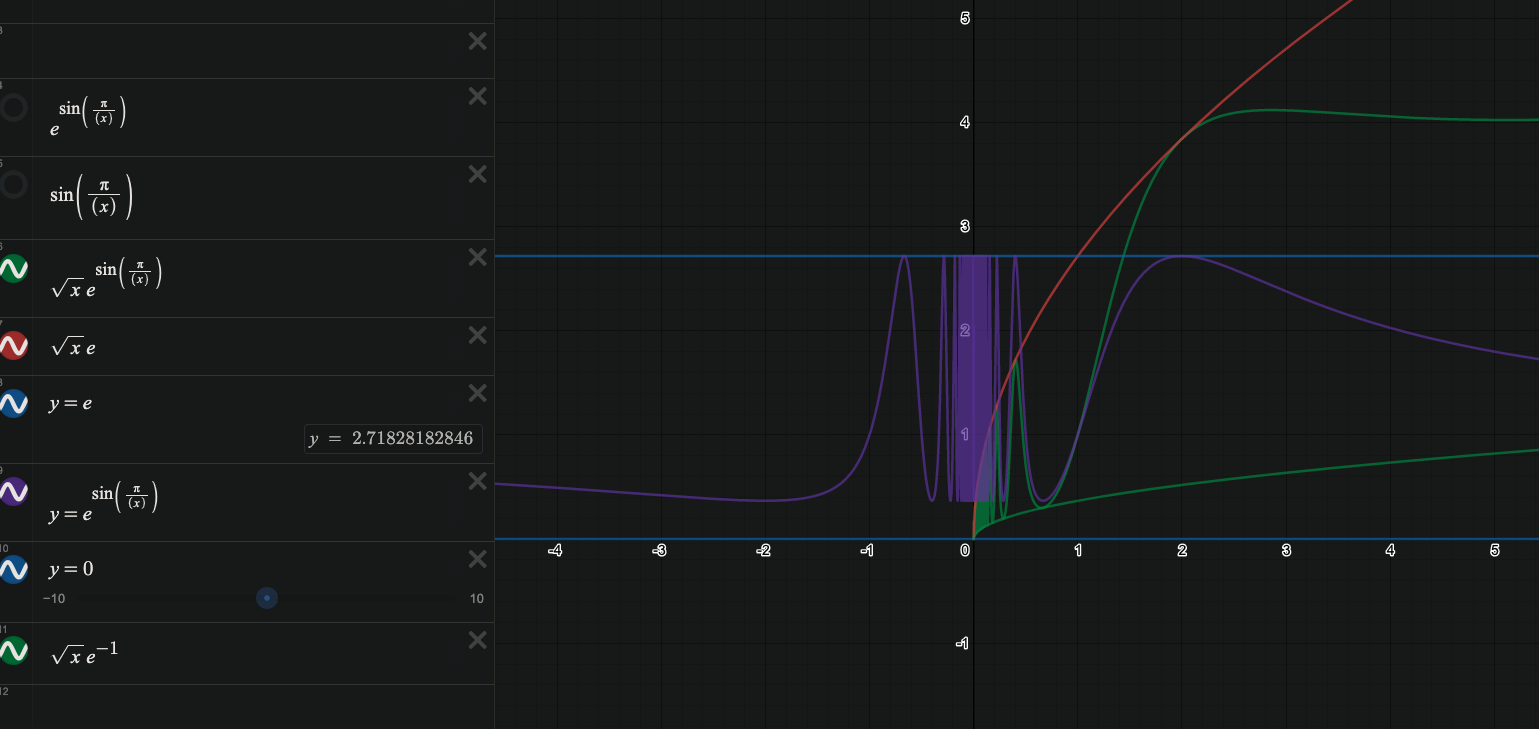
So we know from earlier that \(-1 \le sin\frac{\pi}{x} \le 1\) and like taking a psotivie numebr to a power is not gonn make it negative so like \(e^{sin\frac{\pi}{x}}\) is gonna be more den \(0\)
oh and also because the sin power thingjust makes it fluctuate - we can prolly ignore that entire term and just try \(\sqrt{x}\)
except sike it's too low it needs to be bigger
- maybe just multpily by \(e\) liek \(\sqrt{x}e\)
great so now we have an upper bound and the lower bound is zero so that works except maybe we can make a :sunglasses:-er one? - guess god strats maybe it's the lower bound of the \(\sin{\frac{\pi}{x}}\) exponent so like \(\sqrt{x}e^{-1}\) and yup thats' work guess god strat always wins
Here's the actual "writeup" \[
\begin{aligned} -1 \le sin{\frac{\pi}{x}} \le 1\\ \therefore& e^{-1} \le e^{sin{\frac{\pi}{x}}} \le e^1\\ \therefore& \sqrt{x}e^{-1} \le \sqrt{x}e^{sin\frac{\pi}{x}} \le \sqrt{x} e\\ \lim_{x\to 0^+} \sqrt{x}e^{-1} = \sqrt{0}e^{-1} = 0\\ \lim_{x\to 0^+} \sqrt{x}e = \sqrt{0}e = 0\\ \therefore& \lim_{x\to 0^+}\sqrt{x}e^{sin\frac{\pi}{x}} = \boxed{0} \end{aligned}\] thanks for coming to my ted talk