Backlinks
- lrm;
Table of Contents
1 Limit Laws
see pdf
2 Openstax Calculus Vol1 2.3 Exercises
2.1 84
\[ \lim_{x\to 1}\frac{x^3+3x^2+5}{4-7x} = \frac{1+3+5}{4-7} = \frac{9}{-3} = \boxed{-3} \]
2.2 85
\[ \lim_{x\to -2}\sqrt{x^2-6x+3} = \sqrt{4 - (-12) + 3} = \boxed{\sqrt{19}} \]
2.3 86
\[ \lim_{x\to_1}\left(9x+1\right)^2 = \left(-9+1\right)^2 = \boxed{64} \]
2.4 94
\[
\begin{aligned} \lim_{x\to 4}\frac{x^2-16}{x-4} &= \frac{0}{4-4} = \frac{0}{0}\\ &\Rightarrow \lim_{x\to 2}\frac{\cancel{x-2}}{x\cancel{\left(x-2\right)}} = \lim_{x\to 2}\frac{1}{x} = \boxed{\frac{1}{2}} \end{aligned}\]
2.5 98
\[ \lim_{h\to 0}\frac{\frac{1}{a+h}-\frac{1}{a}}{h} \Rightarrow \frac{ \lim_{h\to 0}\frac{1}{a+h}-\lim_{h\to 0}\frac{1}{a} }{\lim_{h\to 0}h} \]
now what..?
This is just the derivative of \(\frac{1}{a}\) where \(a\) is a real valued, non zero constant. So, it should just be \(\boxed{\frac{-1}{a^2}}\).
2.5.1 In class review
\[\lim_{h\to 0}\frac{\frac{a-a-h}{(a+h)a}}{h} \Rightarrow \lim_{h\to 0}\frac{-1}{a(a+h)}\]
2.6 100
\[ \lim_{x\to1}\frac{x^3-1}{x^2-1} \Rightarrow \lim_{x\to 1}\frac{\cancel{(x-1)}(x^2+1+x)}{(x+1)\cancel{(x-1)}} = \lim_{x\to 1}\frac{x^2+x+1}{x+1} = \boxed{\frac{3}{2}} \]
2.7 Time Check
It's been an 45 minutes. I will now give up on LaTeXing things:
Problem Result 108 2 109 7 110 108 111 \(\sqrt{5}\) 112 36 113 28 114 30 2.8 116
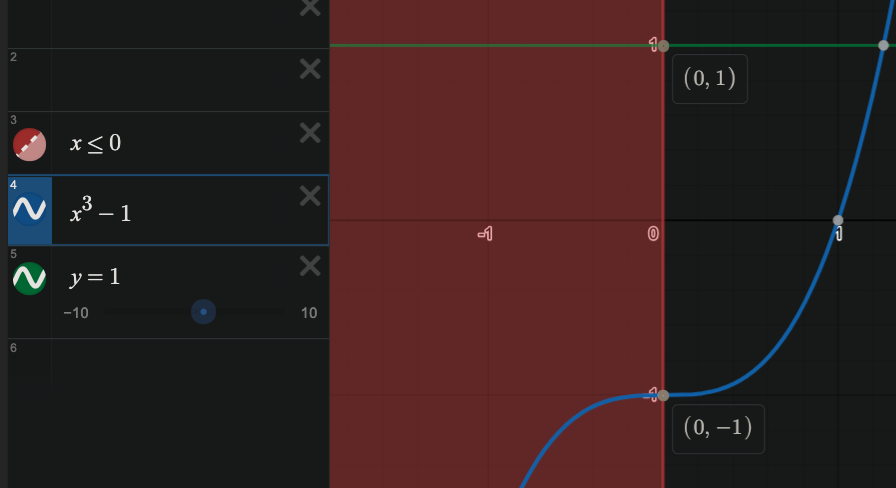
\(\boxed{-1, 1}\)
2.9 Continuity
- Function compositions are continuous if their parts are continuous
- Sum, difference, multiples, powers are continuous if you don't divide by zero or take an even root of a negative