Backlinks
1 Building the Roof
We first begin to construct the general shape of the house' slope, without the leaning bounds. For this, we leverage a hyperbolic parabaloid with an logarithmic component along the \(y\) direction to simulate tapering: \(f(x,y) = \frac{1}{15}x^2 + ln(y)\). Evidently, we crop out dimensions where \(y<1\) to reduce the large, \(-\infty\) trend.
f(x,y) = (1/15)*x^2 + ln(y) plot3d(f, (x,-5,5), (y,1,10))

Based on the image of the construction, we could see that the \(+x\) components is higher than the \(-x\) component, so we shift the x-direction slightly to maintain this.
f(x,y) = (1/15)*x^2 + ln(y) plot3d(f, (x,-4,6), (y,1,10))

Finally, we realize that there are a linear ledge that cuts through this building, which we will simulate by plotting two bound lines:
g = Graphics() f(x,y) = (1/15)*x^2 + ln(y) g += plot3d(f, (x,-4,6), (y,1,10)) g += plot((1/2)*y+1, (y,0,5), thickness=2, color="green") g += plot(-(1/2)*x+1, (x,-4,0), thickness=2, color="blue") g
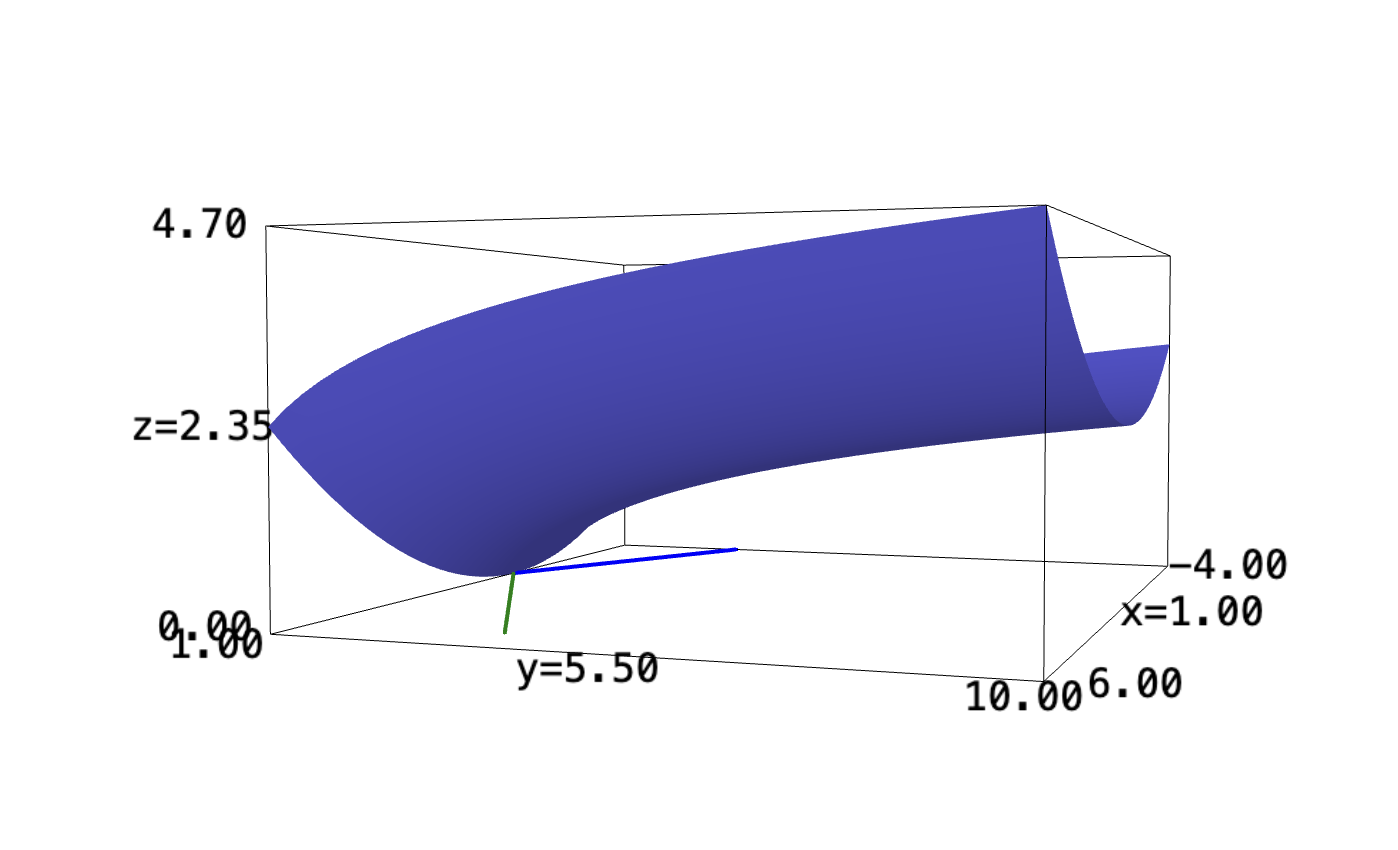
Indeed, that the blue and green lines slice through the function to create its triangular bounds.
2 Slope
What is the slope of the roof?
The slope of the roof is represented as the gradient of the roof function at any point. The function of the roof is:
\begin{equation} f(x,y) = \frac{1}{15}x^2 + ln(y) \end{equation}Therefore, we take the gradient of the function to figure the slope.
\begin{equation} \nabla f = \begin{bmatrix} \frac{2}{15}x \\ \frac{1}{y} \end{bmatrix} \end{equation}Therefore, at any point \((x,y)\), the slope is represented as above. Furthermore, it has an angle of:
\begin{equation} arctan(\frac{15}{2xy}) \end{equation}3 Slope at Center
Suppose you are standing at the exact center of this roof — or, to be a bit more precise, on a spot that's directly over the center of the footprint of the building. What is the slope of the roof at that point?
If we are dealing with the center of the roof, footprint wise, we are actually bound by three functions.
\begin{equation} \begin{cases} y=2x-2 \\ y=\frac{-1}{2}x+1 \\ y=10 \\ \end{cases} \end{equation}We calculate the three point of intersections between these three lines.
\begin{equation} \begin{cases} (6, 10) \\ (\frac{6}{5}, \frac{2}{5}) \\ (-18, 10) \end{cases} \end{equation}Therefore, we need to find the center of the object as bounded by these two points.
The x-bounds are \([-18, 6]\), and the y-bounds are \([\frac{2}{5}, 10]\). The centre therefore, are the average of these points: namely, \((\frac{-44}{5}, 8)\).
We then apply these coordinates to the gradient function to figure the slope at the center.
\begin{equation} \nabla f(\frac{-44}{5}, 8) = \begin{bmatrix} \frac{-88}{75} \\ \frac{1}{8} \end{bmatrix} \end{equation}4 Slope at Middle
Suppose you are standing in the same spot, facing directly towards the middle of one of the shorter-length sides. What is the slope at that point, in that direction?
One of the sides is defined by the following expression:
\begin{equation} y = 2x-2 \end{equation}It is, furthermore, bounded by \(0 \leq x \leq 6\), as the maximum \(y\) value of the function is \(y=10\); therefore, solving the expression for \(x\) results in the new \(y\) value of \(10\).
Halfway through the bounds, therefore, is \(x=3\). Therefore, it is towards the point \((3, 4)\); we are currently located at \((\frac{-44}{5}, 8)\), therefore the vector difference between the two points:
\begin{equation} \begin{bmatrix} \frac{59}{5}\\ -4 \end{bmatrix} \end{equation}We will now normalize this vector:
\begin{equation} \begin{bmatrix} \frac{59}{3881\sqrt{ 3881 }}\\ \frac{-20}{3881\sqrt{ 3881 }} \end{bmatrix} \end{equation}Finally, we will then project our gradient as calculated above upon this normalized vector:
\begin{equation} \begin{bmatrix} \frac{59}{3881\sqrt{ 3881 }}\\ \frac{-20}{3881\sqrt{ 3881 }} \end{bmatrix} \cdot \begin{bmatrix} \frac{-88}{75} \\ \frac{1}{8} \end{bmatrix} = \frac{10009}{582150 \sqrt{3881}} \end{equation}We then scale the normalized direction vector with this magnitude:
\begin{equation} \begin{bmatrix} \frac{590531}{2259324150} \\ \frac{-20018}{225932415} \end{bmatrix} \end{equation}This was surprisingly lengthy value-wise, though it is actually quite a small value. This makes sense, as the "horizontal" direction slope is very flat.
5 Slope at a corner
Suppose you are standing in the same spot, facing towards one of the corner of the roof. What is the slope at that point, in that direction?
We note that the intersections of the bound lines forms the "front" corner of the roof at \((\frac{6}{5}, \frac{2}{5})\). We further note that we are currently located at \((\frac{-44}{5}, 8)\). Therefore, we find the vector difference between these two points:
\begin{equation} \begin{bmatrix} 10 \\ \frac{-38}{5} \end{bmatrix} \end{equation}We now normalize this vector:
\begin{equation} \begin{bmatrix} \frac{25}{986 \sqrt{986}} \\ \frac{-19}{986 \sqrt{986}} \\ \end{bmatrix} \end{equation}We finally project this vector upon our gradient:
\begin{equation} \begin{bmatrix} \frac{25}{986 \sqrt{986}} \\ \frac{-19}{986 \sqrt{986}} \\ \end{bmatrix} \cdot \begin{bmatrix} \frac{-88}{75} \\ \frac{1}{8} \end{bmatrix} = \frac{-761}{23664\sqrt{ 986 }} \end{equation}and finally, scale the normalized direction vector by this magnitude:
\begin{equation} \begin{bmatrix} \frac{-19025}{23664} \\ \frac{14459}{23664} \\ \end{bmatrix} \end{equation}6 Orthogonal Vector
Suppose you are standing in the same spot, and you want to face in the direction such that the roof is flat. What direction do you face in?
To make the direction of the roof flat, we go in the negative-reciprocal direction of the gradient vector; that:
\begin{equation} \begin{bmatrix} \frac{1}{8} \\ \frac{88}{75} \\ \end{bmatrix} \end{equation}We could verify that this vector is indeed flat at that point by applying the dot product to the original gradient vector:
\begin{equation} \begin{bmatrix} \frac{1}{8} \\ \frac{88}{75} \\ \end{bmatrix} \cdot \begin{bmatrix} \frac{-88}{75} \\ \frac{1}{8} \end{bmatrix} = 0 \end{equation}This direction, therefore, would represent a direction for a flat root.