Backlinks
Table of Contents
One possible design for one side of the roof would be a simple cubic function; that:
\begin{equation} f(x,y) = \frac{1}{8} x^3 \{0 \leq x \leq 4, -5 \leq y \leq 5\} \end{equation}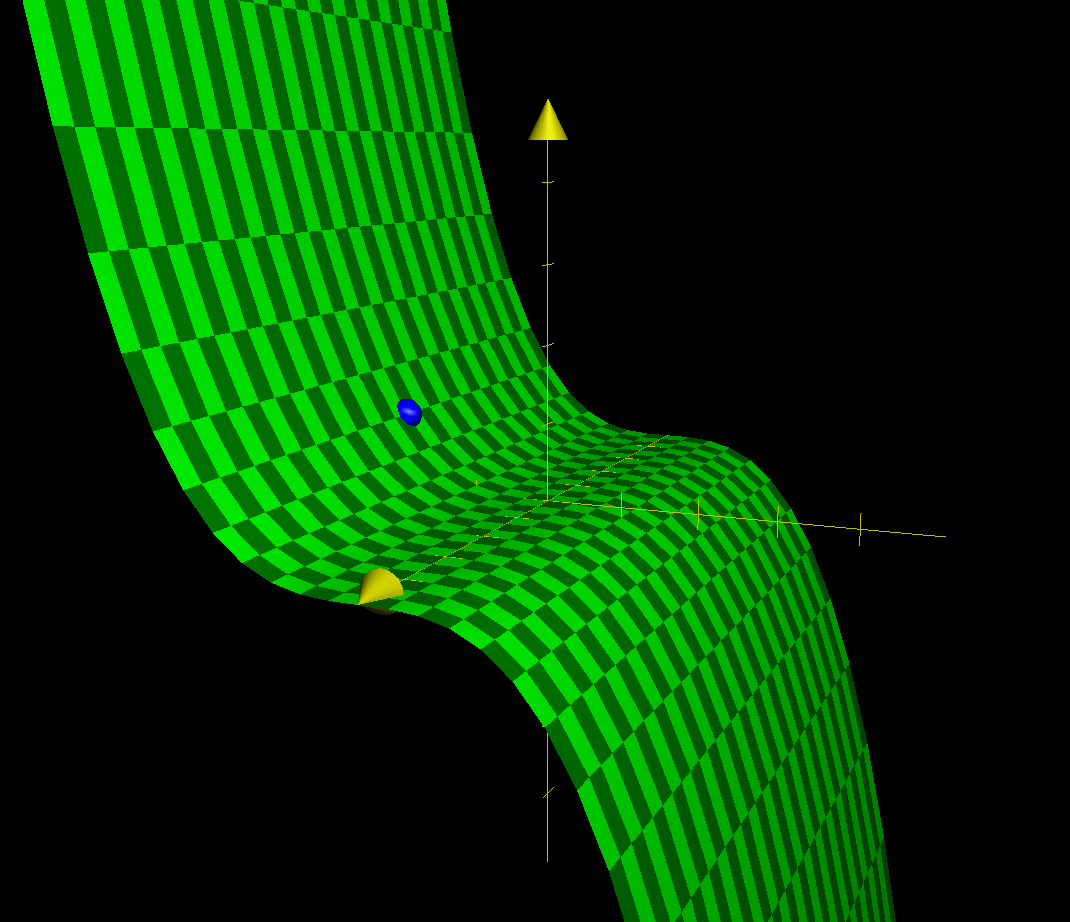
1 Slope in Middle
The "middle" of the roof, therefore, is the location \((2,0)\), as indicated by the blue dot above.
Standing in the middle, and facing the "ridge" (\(+x\)) direction, we could calculate the slope of the roof.
The vector facing the ridge of the roof, to the positive \(x\) direction, is represented by
\begin{equation} \begin{bmatrix} 1 \\ 0 \end{bmatrix} \end{equation}the gradient of this function is represented by:
\begin{equation} \begin{bmatrix} \frac{3}{8}x^2 \\ 0 \end{bmatrix} \end{equation}Therefore, at the center point as indicated, the gradient is:
\begin{equation} \begin{bmatrix} 6 \\ 0 \end{bmatrix} \end{equation}Computing the dot product of the direction and the gradient as found, we arrive that — at the center — the slope is:
\begin{equation} \begin{bmatrix} 1 \\ 0 \end{bmatrix} \cdot \begin{bmatrix} 6 \\ 0 \end{bmatrix} = 6 \end{equation}Therefore, the slope as indicated is \(6 \approx 80.5^{\circ}\).
2 Facing the Peak
We first determine a vector that originates from the center of the roof, and facing towards one of the ridges; that:
\begin{equation} \begin{bmatrix} 4 \\ 5 \end{bmatrix} - \begin{bmatrix} 2 \\ 0 \end{bmatrix} = \begin{bmatrix} 2 \\ 5 \end{bmatrix} \end{equation}Normalizing this vector, we arrive at:
\begin{equation} \begin{bmatrix} \frac{2}{\sqrt{29}} \\ \frac{5}{\sqrt{29}} \\ \end{bmatrix} \end{equation}We will then project the gradient at the center point atop this vector:
\begin{equation} \begin{bmatrix} \frac{2}{\sqrt{29}} \\ \frac{5}{\sqrt{29}} \\ \end{bmatrix} \cdot \begin{bmatrix} 6 \\ 0 \end{bmatrix} = \frac{12}{\sqrt{29}} \end{equation}Therefore, the slope as indicated is \(\frac{12}{\sqrt{29}} \approx 65.83^{\circ}\).
3 Maximizing the Angle
To face in the steepest direction, we will need to face the direction of the gradient. As the gradient is
\begin{equation} \begin{bmatrix} 6 \\0 \end{bmatrix} \end{equation}as derived above, the direction of the gradient is therefore:
\begin{equation} \begin{bmatrix} \frac{6}{6} \\0 \end{bmatrix} = \begin{bmatrix} 1 \\0 \end{bmatrix} \end{equation}