Backlinks
1 Roofs, Antecedent
Consider the point \((5,7)\). Using trig, complex numbers, etc., rotate it \(62.8^{\circ}\) counterclockwise.
We first begin by, given a \(\theta\) and a vector \(v \in \mathbb{R}^2 = (x,y)\), deriving the counter-clockwise rotation matrix such that \(v\) would be rotated by \(\theta\) degrees counter-clockwise.
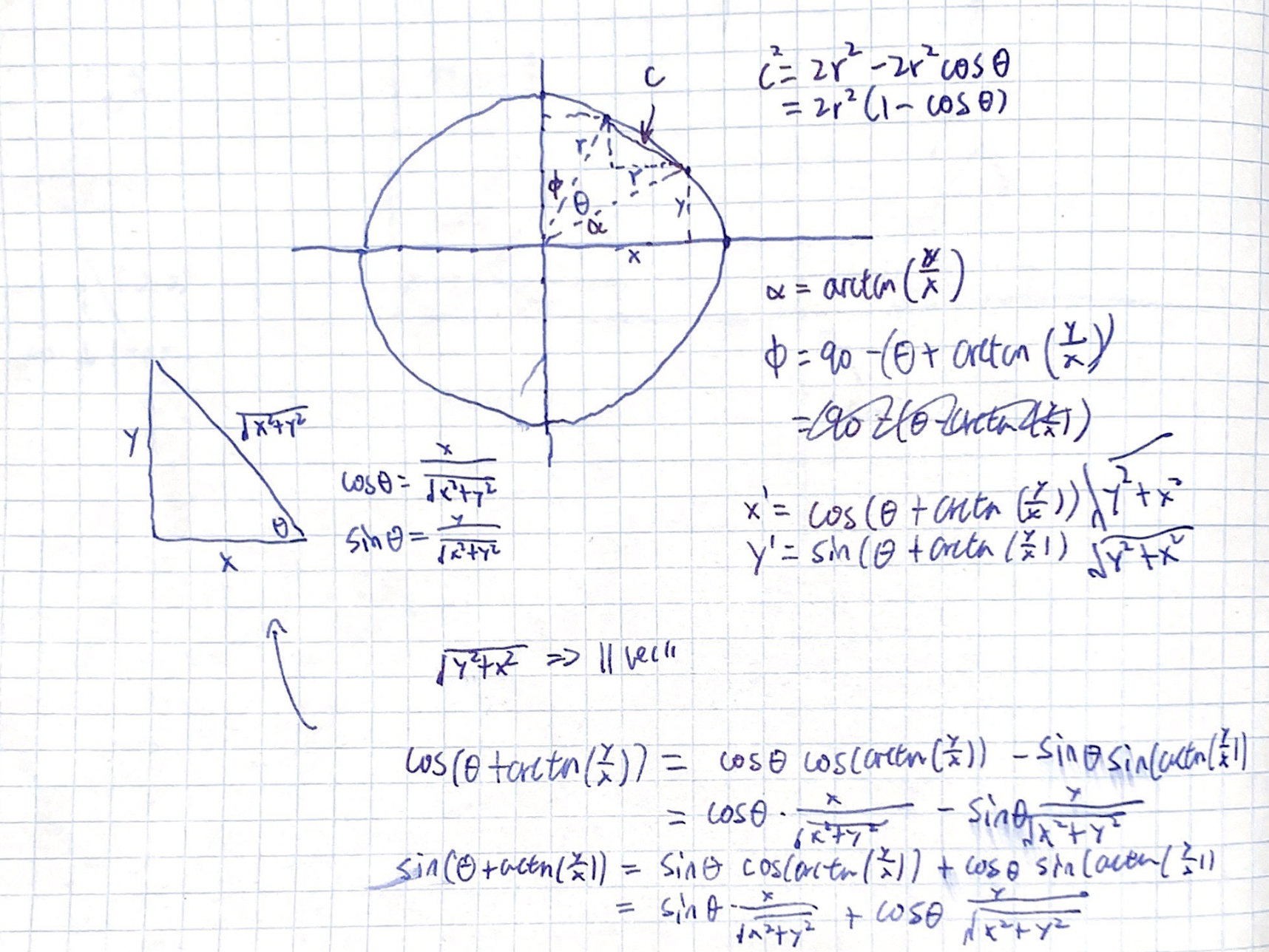
We begin by setting up the angles by which the problem is constructed: that, based on figuring of angles \(\phi\), \(\alpha\), and given \(\theta\), we could derive expression for the new positions of \(x\) and \(y\).
Expanding the expressions, we arrive at the fact that:
\begin{equation} \begin{cases} x' = \sqrt{x^2+y^2} (cos(\theta) cos(arctan(\frac{y}{x})) - sin(\theta)sin(arctan(\frac{y}{x}))) \\ y' = \sqrt{x^2+y^2} (sin(\theta) cos(arctan(\frac{y}{x})) + cos(\theta)sin(arctan(\frac{y}{x}))) \end{cases} \end{equation}Per the observation of the above-illustrated right triangle, we derive that:
\begin{equation} \begin{cases} cos(arctan(\frac{y}{x})) = \frac{x}{\sqrt{x^2+y^2}}\\ sin(arctan(\frac{y}{x})) = \frac{y}{\sqrt{x^2+y^2}} \end{cases} \end{equation}Substituting these values in the above-derived expression, we arrive at that:
\begin{equation} \begin{cases} x' = \sqrt{x^2+y^2} (cos(\theta) \frac{x}{\sqrt{x^2+y^2}} - sin(\theta)\frac{y}{\sqrt{x^2+y^2}}) \\ y' = \sqrt{x^2+y^2} (sin(\theta) \frac{x}{\sqrt{x^2+y^2}} + cos(\theta)\frac{y}{\sqrt{x^2+y^2}}) \end{cases} \end{equation}Simplifying slightly, we arrive at that:
\begin{equation} \begin{cases} x' = (xcos(\theta) - ysin(\theta)) \\ y' = (xsin(\theta) + ycos(\theta)) \end{cases} \end{equation}Evidently, this could be mapped easily as a linear transformation \(T\) upon the vector \((x,y)\):
\begin{equation} \begin{bmatrix} x \\ y \end{bmatrix} T = \begin{bmatrix} x \\ y \end{bmatrix} \begin{bmatrix} cos\theta & -sin\theta \\ sin\theta & cos\theta \\ \end{bmatrix} = \begin{bmatrix} xcos\theta - ysin\theta \\ xsin\theta + ycos\theta \\ \end{bmatrix} \end{equation}Therefore, the linear transformation which match the needed parameters is:
\begin{equation} \begin{bmatrix} cos\theta & -sin\theta \\ sin\theta & cos\theta \\ \end{bmatrix} \end{equation}Finally, we apply the linear transformation to the numerical values supplied to rotate the vector:
\begin{equation} \begin{bmatrix} 5 \\ 7 \end{bmatrix} \begin{bmatrix} cos(62.8^{\circ}) & -sin(62.8^{\circ}) \\ sin(62.8^{\circ}) & cos(62.8^{\circ}) \end{bmatrix} = \begin{bmatrix} xcos\theta - ysin\theta \\ xsin\theta + ycos\theta \\ \end{bmatrix} \approx \begin{bmatrix} -3.94\\ 7.65 \end{bmatrix} \end{equation}2 Slopes with Temperature
Suppose the temperature at any point \((x,y,z)\) is given by:
\begin{align} &T : \mathbb{R}^3 \to \mathbb{R}^1 \\ &T(x,y,z) = 12xyz + 1 (kelvin) \end{align}Suppose you are standing at point \((1,1,1)\).
2.1 Increasing Temperature
If you want to increase your temperature as fast as possible, in what direction should you move?
To increase the temperature as fast as possible, we move along the direction of the gradient. We will proceed to derive the gradient of the function:
\begin{equation} \nabla T = \begin{bmatrix} 12yz \\ 12xz \\ 12xy \end{bmatrix} \end{equation}At the point \((1,1,1)\), therefore, the gradient is:
\begin{equation} \nabla T = \begin{bmatrix} 12 \\ 12 \\ 12 \end{bmatrix} \end{equation}Evidently, the direction matrix corresponding to this, normalized is:
\begin{equation} \nabla T = \begin{bmatrix} \frac{1}{3\sqrt{3}} \\ \frac{1}{3\sqrt{3}} \\ \frac{1}{3\sqrt{3}} \end{bmatrix} \end{equation}Hence, to move in the direction in the steepest descend, move along in the direction above.
2.2 Rate of Change of Steepest Descent?
What is the rate of change in that direction?
The rate of change of moving along that direction is 1-by-1-by-1: that for every unit moved in any dimension, one unit will be moved in any other direction.
2.3 Move but maintain current temperature?
If you wast to move, but maintain your current temperature, in which direction should you move?
In this case, we wish to move in a direction such that we would exactly counter the gradient at that point. That is, we wish to find a vector whose dot product with the gradient at that point would be zero (orthogonal to this vector): that
\begin{equation} \begin{bmatrix} 13 \\ 13 \\ 13 \end{bmatrix} \cdot \begin{bmatrix} a \\ b \\ c \end{bmatrix} = 13a + 13b + 13c = 0 \end{equation}One possible solution to this is \(a=1\), \(b=0\), \(c=-1\): making the vector
\begin{equation} \begin{bmatrix} 1 \\ 0 \\ -1 \end{bmatrix} \end{equation}orthogonal to the original direction vector and also the direction with zero change in temperature.