Backlinks
You are driving dangerously. Your position, as a function of time, at any point \(t\) is:
\begin{align} &f: \mathbb{R}^2 \to \mathbb{R}^2 \\ &f(t) = \begin{bmatrix} t^2 - 9 \\ 12sin(t) + t \end{bmatrix} \end{align}
1 Image of the Adventure
Draw a map of the adventure!
f(t) = (t^2-9, 12*sin(t) + t, t) parametric_plot3d(f, (t, -5, 5), thickness=5)
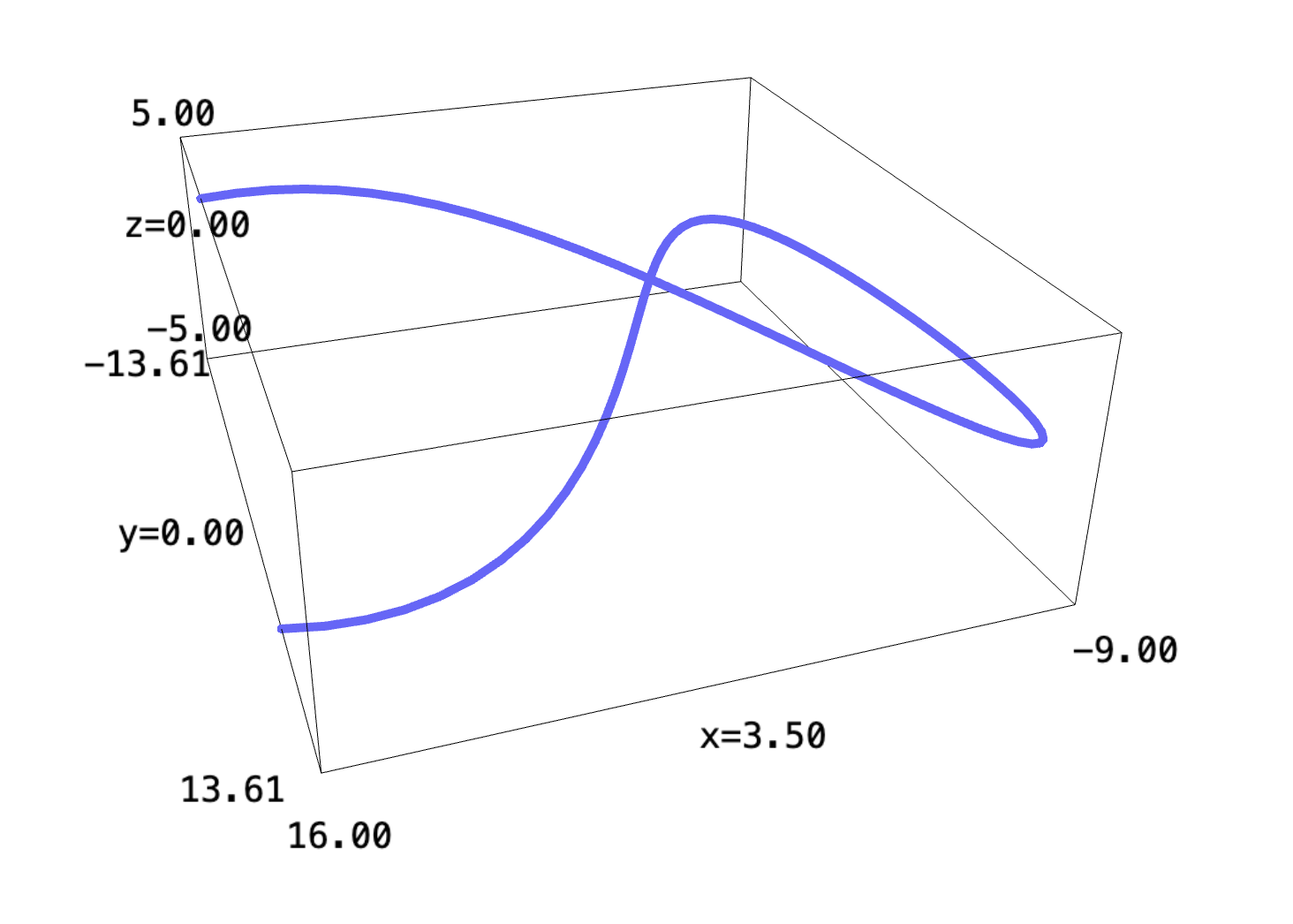
2 Velocity
\begin{equation} \nabla f(t) = v(t) = \begin{bmatrix} 2t \\ 12cos(t) +1 \end{bmatrix} \end{equation}What is your velocity, as a function of time?
v(t) = (2*t, 12*cos(t) +1, t) parametric_plot3d(v, (t, -5, 5), thickness=5)
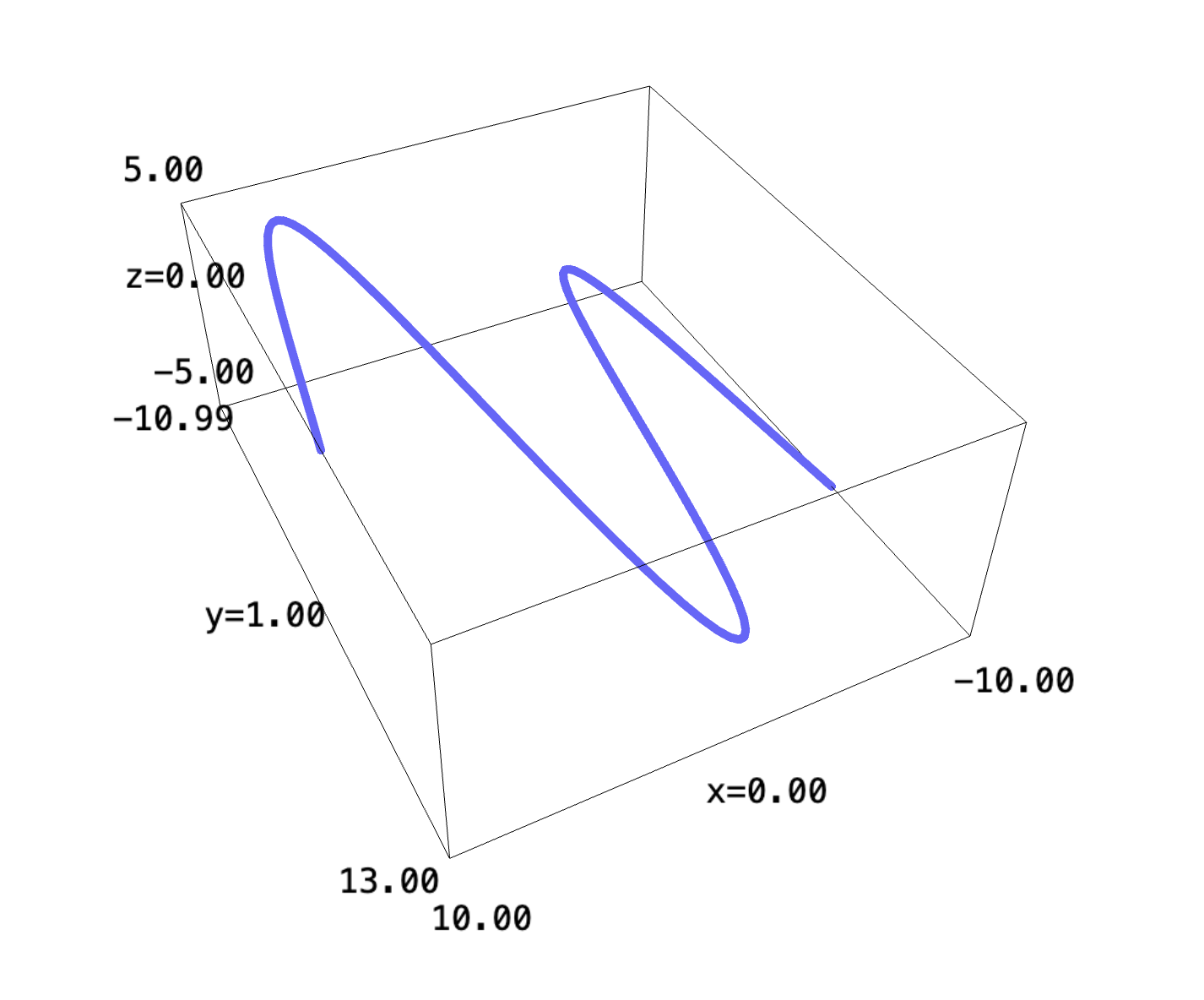
3 Acceleration
\begin{equation} \nabla v(t) = a(t) = \begin{bmatrix} 2 \\ -12sin(t) \end{bmatrix} \end{equation}What is your acceleration, as a function of time?
a(t) = (2, -12*sin(t), t) parametric_plot3d(a, (t, -5, 5), thickness=5)
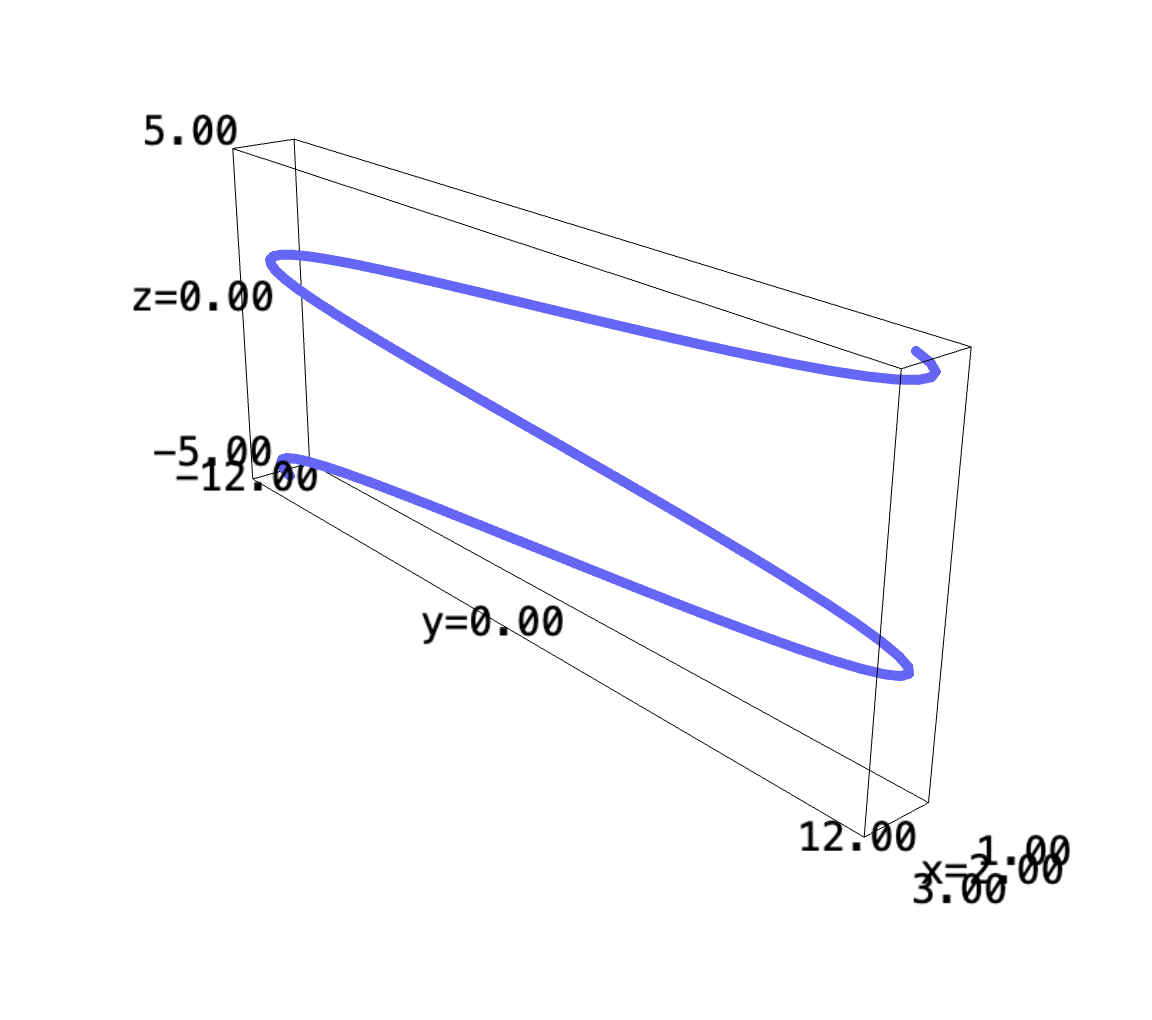
4 At \(t=\pi\), how fast are you going + how fast are you accelerating?
At \(t=\pi\), the velocity vector is as follows:
\begin{equation} v(\pi) = \begin{bmatrix} 2\cdot \pi \\ 12cos(\pi) +1 \end{bmatrix} = \begin{bmatrix} 2\pi \\ -11 \end{bmatrix} \end{equation}Therefore, taking the magnitude of this vector, we arrive at that:
\begin{equation} \sqrt{(2\pi)^2 + (-11)^2} \approx 12.668 \end{equation}is the speed at \(t = \pi\).
Furthermore, at \(t = \pi\), the acceleration of the vector is as follows:
\begin{equation} a(\pi) = \begin{bmatrix} 2 \\ -12 sin(\pi) \end{bmatrix} = \begin{bmatrix} 2 \\ 0 \end{bmatrix} \end{equation}Therefore, the magnitude of acceleration is:
\begin{equation} \sqrt{2^2} = 2 \end{equation}5 Optimizing for Velocity
To figure the fastest speed at which we would go, we would need to optimize the function of speed w.r.t. \(t\).
The velocity vector, as derived above, is:
\begin{equation} v(t) = \begin{bmatrix} 2t \\ 12cos(t) +1 \end{bmatrix} \end{equation}Therefore, the magnitude of the velocity is:
\begin{align} &\sqrt{4t^2 + (12cos(t)+1)^2} \\ =&\sqrt{4t^2 + (12cos(t)+1)^2} \\ =&\sqrt{4t^2 + 144cos^2(t) + 24cos(t) + 1} \end{align}We wish to optimise this expression for the most optimal value such that this expression would be maximised. We realise that \(cos(t)\) and \(sin(t)\) are both sinsodial functions, but \(4t^2\) is a quadratic function that increases infinitely as \(t\) increases.
Therefore, we recognize that:
\begin{equation} \lim_{t \to \infty} \sqrt{4t^2 + 144cos^2(t) + 24cos(t) + 1} = \infty \end{equation}Therefore, there is no limit to the maximum speed which one could achieve under this expression.
6 Optimizing to Acceleration
We similarly figure the function for the magnitude of speed w.r.t. \(t\).
\begin{equation} a(t) = \begin{bmatrix} 2 \\ -12sin(t) \end{bmatrix} \end{equation}Therefore, the magnitude of acceleration is:
\begin{equation} \sqrt{4 + 144sin^2(t)} \end{equation}We could proceed to take the single-variable derivative of this expression w.r.t. \(t\) and solve for positions at which it would be 0 to figure the critical points, and, eventually maximum magnitude of acceleration.
\begin{align} &\frac{d}{dt} \sqrt{4 + 144sin^2(t)} = 0 \\ \Rightarrow & \frac{288sin(t)cos(t)}{2\sqrt{4 + 144sin^2(t)}} = 0 \\ \Rightarrow & \frac{144sin(t)cos(t)}{\sqrt{4 + 144sin^2(t)}} = 0 \\ \Rightarrow & \frac{72sin(2t)}{\sqrt{4 + 144sin^2(t)}} = 0 \end{align}Therefore, we could derive that critical points of this function exists at:
\begin{equation} t = \{0, \frac{\pi}{2}, -\frac{\pi}{2}\} \end{equation}As, at those positions, the expression \(72 sin(2t)\) would be \(0\), making the above expression \(0\).
Supplying these expressions into the expression for acceleration, we could derive that:
\begin{equation} a(\{0, \frac{\pi}{2}, -\frac{\pi}{2}\}) \approx \{2, 12.165, 12.165\} \end{equation}We derive that the function is maximized at \(t=\{\frac{\pi}{2}, \frac{-\pi}{2}\}\), and the maximum velocity attainable is \(12.165 \frac{m}{s^2}\).
The maximum survivable acceleration is \(9g \approx 88.25\), which this value is well below. Hence, it is survivable by a human.
7 Integration of Travel
As the distance is simply the integration of the magnitude of velocity, we need to figure the distance of the course of the journey via taking the definite integral of the magnitude of velocity as derived above:
\begin{equation} \int^{3\pi}_{-2\pi} \sqrt{4t^2 + 144cos^2(t) + 24cos(t) + 1} dt \end{equation}Unfortunately, this is not an expression that is possible to be trignometrically substituted to integrate (as there is a \(+1\) term that prevents the completion of a square). Numerically, the individual travelled for roughly \(189.668\) metres.