Backlinks
Table of Contents
1 Taylor Series in \(e^x\)
\begin{equation} f(x) = e^x = e^2 + e^2(x-2) + \frac{e^2(x-2)^2}{2!} + \frac{e^2(x-2)^3}{3!} \cdots + \frac{e^2(x-2)^n}{n!} \end{equation}Calculate, from the big scary formula, the Taylor series for \(e^x\), centered around \(x=2\).
2 Diff. in Higher Dimensions
2.1 Derivative Matrix 14
\begin{equation} f'(x_1,x_2,x_3,x_4) = \begin{bmatrix} x_3 & 0 & x_1 & 0\\ 0 & 0 & 0 & \sec^2(x_4)\\ 0 & \frac{-1}{x_2} & 0 & 0\\ 12(3x_1-2)^3 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \end{bmatrix} \end{equation}Find the derivative matrix of
\begin{equation} f:\mathbb{R}^4 \to \mathbb{R}^5; f(x_1,x_2,x_3,x_4) = \begin{bmatrix} x_1 x_3 \\ \tan(x_4) \\ -\ln(x_2) \\ (3x_1-2)^4 \\ 1729 \end{bmatrix} \end{equation}
2.2 Facing an Arbitrary Direction
Suppose you have a function \(f(x,y); f:\mathbb{R}^2 \to \mathbb{R}^1\). Imagine you are standing at this function, at the point \((x,y)\), facing \(\theta\). What is the slope? For what value is the slope greatest? Upwards? Downwards? Flat?
2.2.1 Slope at point \(\theta\)
The slope at angle \(\theta\) is as follows:
\begin{equation} f_x (x,y) \cos(\theta) + f_y (x,y) \sin(\theta) \end{equation}This simply acts to project the components of the gradient of \(f\) upon its axis \(x\) and \(y\) – \(\cos(\theta)\) and \(\sin(\theta)\) respectively – and sum them into one scalar value.
2.2.2 Greatest slope Upwards
The process to find the angle \(\theta\) at which to maximize the slope requires optimizing the above-derived expression. As we know that there exists a \(\theta\) such that the slope would be maximized, we could perform this by solving for \(\theta\) on the following expression:
\begin{equation} \frac{d}{d\theta}( f_x (x,y) \cos(\theta) + f_y (x,y) \sin(\theta)) = 0 \end{equation}Solution of this expression would therefore be the angle at which the slope is maximized. Hence, we solve for \(\theta\) in the above expression.
\begin{align} &\frac{d}{d\theta}( f_x (x,y) \cos(\theta) + f_y (x,y) \sin(\theta)) = 0 \\ \Rightarrow &-f_x(x,y) \sin(\theta) + f_y (x,y) \cos(\theta) = 0 \\ \Rightarrow & f_y (x,y) \cos(\theta) = f_x(x,y) \sin(\theta) \\ \Rightarrow & \frac{f_y (x,y)}{f_x(x,y)} = \frac{\sin(\theta)}{\tan(\theta)} \\ \Rightarrow & \frac{f_y (x,y)}{f_x(x,y)} = \tan(\theta) \\ \Rightarrow & \theta = \arctan(\frac{f_y (x,y)}{f_x(x,y)}) \end{align}The unit direction vector representing this slope, therefore, would be:
\begin{equation} \begin{bmatrix} \frac{f_x(x,y)}{\sqrt{{f_x}^2(x,y)+{f_y}^2(x,y)}} \\ \frac{f_y(x,y)}{\sqrt{{f_x}^2(x,y)+{f_y}^2(x,y)}} \\ \end{bmatrix} \end{equation}2.2.3 Greatest slope Downwards
Given the max \(\theta\) as derived above:
\begin{equation} \pi - \theta \end{equation}The vector orthogonal to the vector direction representing the maximum slope will represent the smallest slope.
The vector representing this expression, therefore, would be
\begin{equation} \begin{bmatrix} \cos(\pi - \theta) \\ \sin(\pi - \theta) \\ \end{bmatrix} \end{equation}2.2.4 Angle of Flat Slope
To figure the angle at which a flat slope exists, we simply solve for an expression for \(\theta\) while setting the above-derived expression for slope-at-angle at \(0\) as that would represent a flat slope.
\begin{align} & f_x (x,y) \cos(\theta) + f_y (x,y) \sin(\theta) = 0 \\ & \Rightarrow f_y (x,y) \sin(\theta) = -f_x (x,y) \cos(\theta) \\ & \Rightarrow \frac{-f_x (x,y)}{f_y (x,y)} = \frac{\sin(\theta)}{\cos(\theta)} \\ & \Rightarrow \frac{-f_x (x,y)}{f_y (x,y)} = \tan(\theta) \\ & \Rightarrow \theta = \arctan{\frac{-f_x (x,y)}{f_y (x,y)}} \end{align}3 Sand Dunes
You are trudging across a field of sand dunes, which the prevailing winds have blown into perfect, parallel, straight lines (or straight ridges, rather). You know that if you walk directly north-northeast, you'll make it to the oasis city of Iskendrebad. The landscape follows the function \(f(x,y) = \sin(x)\); you're at the point with \(x\) coordinate \(23\pi/3\) and \(y\) coordinate \(37\).
3.1 Make a Picture of the Situation
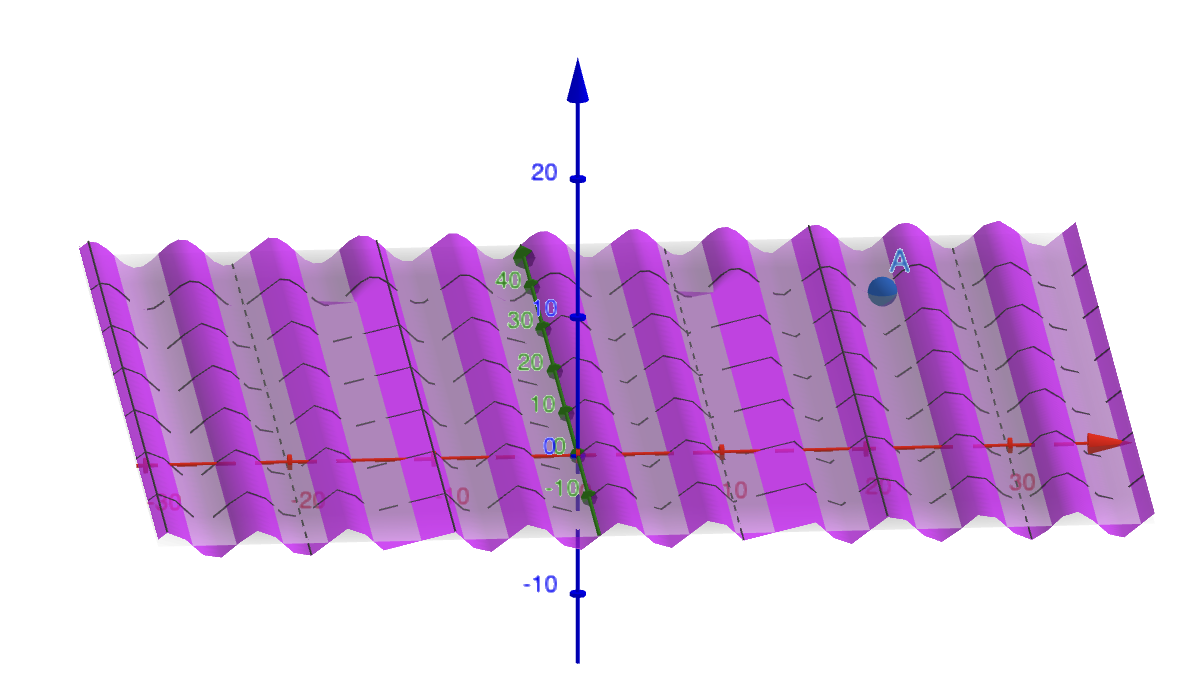
3.2 What is your elevation
At that point, you are at an elevation of \(\sin(\frac{23 \pi}{3}) = \frac{-\sqrt{3}}{2}\)
3.3 What does your hike look like?
"North-northeast" could translate an angle of roughly \(68^{\circ} \approx 0.0174533\ rad\). Slicing though the manifold with a line \(y=2.475x\), which represents the same angle…
We first parameterize the slice equation as follows:
\begin{align*} &y = t \\ &x = \frac{1}{2.475} t \end{align*}The function at \(f(\frac{t}{2.475},t)\), therefore, is:
\begin{equation} f(\frac{t}{2.475},t) = \sin(\frac{t}{2.475}) \end{equation}Hence, the hike will also behave as \(f(t) = \sin(\frac{t}{2.475})\).
This could also be understood as the line at which \(y=2.475x\) intersects with \(z = \sin(x)\). We could solve for the expression w.r.t. setting \(x\) values equal.
\begin{align} y=2.475x \\ \Rightarrow x = \frac{y}{2.475} \\ \Rightarrow z = \sin(\frac{y}{2.475}) \end{align}3.4 What's the function for the slope along your hike?
The function for the slope along the hike is the single-variable derivative of the parametrized function above; that is:
\begin{equation} f'(t) = \frac{d}{dt} \sin(\frac{t}{2.475}) = \frac{1}{2.475} \cos(\frac{t}{2.475}) \end{equation}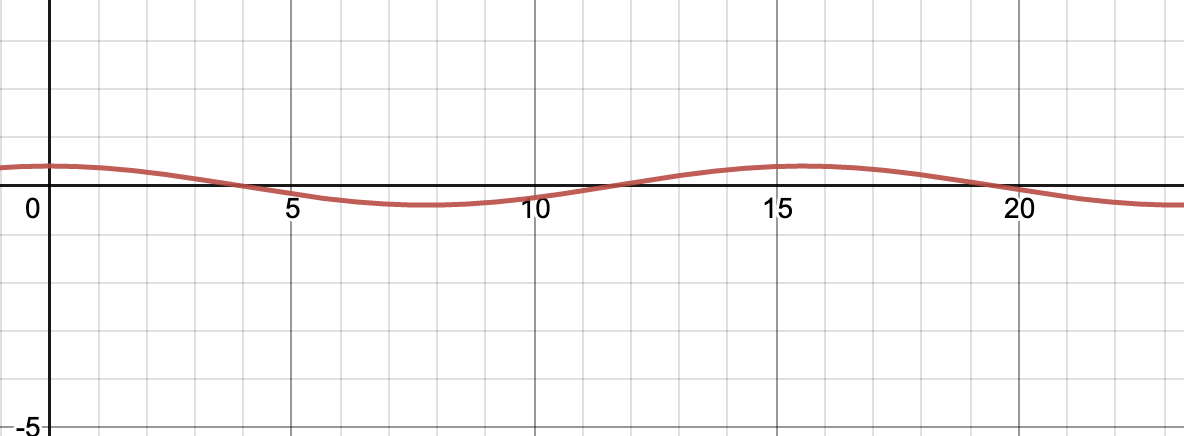
3.5 How steep is the sand dune at the point you're standing (in the direction you're hiking)?
As per above, the direction in which we are standing is at \(68^{\circ}\). This would represent a direction vector of:
\begin{equation} \begin{bmatrix} 0.374606 \\ 0.927183 \end{bmatrix} \end{equation}The gradient of the function at point at \((\frac{23\pi}{3}, 37)\):
\begin{equation} \begin{bmatrix} -\frac{1}{2} \\ 0 \end{bmatrix} \end{equation}Therefore, the slope at that point is:
\begin{equation} \begin{bmatrix} 0.374606 \\ 0.927183 \end{bmatrix} \cdot \begin{bmatrix} -\frac{1}{2} \\ 0 \end{bmatrix} = -0.1873032967 \end{equation}This would amount to a slope of \(\arctan(-0.1873032967) \approx -10.609^{\circ}\)