Backlinks
Table of Contents
1 A surface integral
We are defining a function:
\begin{equation} f(x,y,z) = y^2 \end{equation}and slicing out a vertical organ pipe shape with a sliced edge. That is:
\begin{equation} x^2 + z^2 = 1 \end{equation}bounded by \(y>0\) and \(y<3-x\).
Let's plot this:
var('x,y,z')
f = y^2
implicit_plot3d(x^2+z^2 == 1, (x,-1,1), (y,0,4), (z, -1,1), region=(lambda x,y,z: y>0 and y<3-x), color=(f,colormaps.cool), plot_points=100)
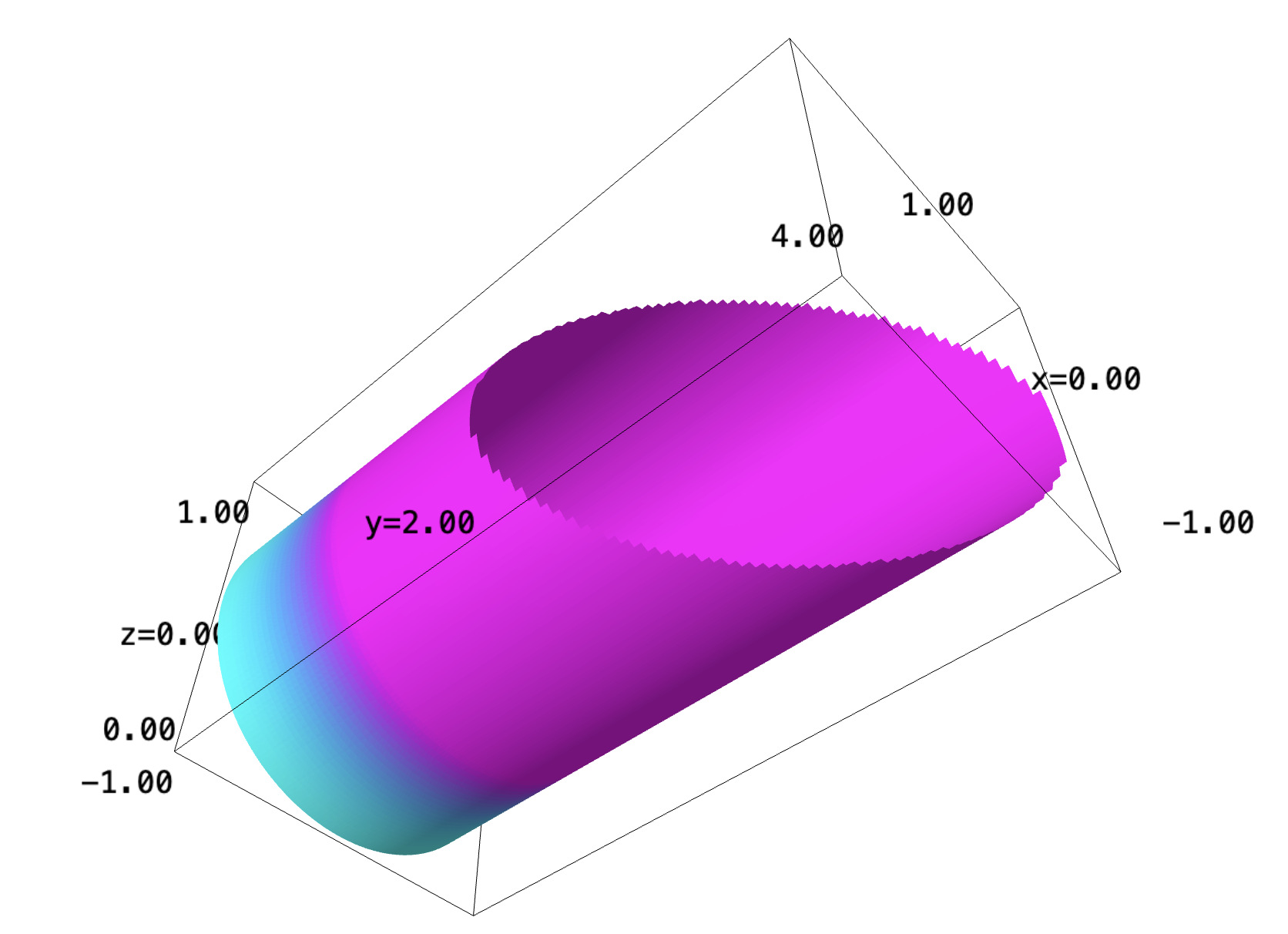
that's honestly pretty cool!
Great, now let's take the actual surface integral. Note that, because the "pipe" does not have a defining ending point, we will set its end at the \(xy\) plane, that it ends at \(x=0\) at the other end in addition to \(y=3-x\).
Looking at the actual function for which we are taking the integral, we have:
\begin{equation} x^2 + z^2 = 1 \end{equation}We will rearrange this expression in terms of \(z\):
\begin{equation} z = \sqrt{1-x^2} \end{equation}Fortunately, we see already that the function's derivative w.r.t. \(y\) is \(0\); indeed, it doesn't change along the \(y\) direction (the cylinder is centered around it after all.)
Taking the derivative in the \(x\) direction:
\begin{align} \frac{\partial z}{\partial x} &= \frac{\partial}{\partial x} \sqrt{1-x^2} \\ &= \frac{-2x}{2\sqrt{-x^2+1}}\\ &= \frac{-x}{\sqrt{-x^2+1}} \end{align}Squaring the expression below:
\begin{equation} \frac{x^2}{-x^2+1} \end{equation}And finally, we have the correction factor:
\begin{align} dA &= \sqrt{\frac{x^2}{-x^2+1} + 1}\ dV\\ &= \sqrt{\frac{1}{-x^2+1}}\ dV \end{align}Lastly, we can multiply the actual value function to this to this expression to get the expression for the integral:
\begin{equation} \iint_V\ y^2\ \sqrt{\frac{1}{-x^2+1}}\ dx\ dy \end{equation}Furthermore, our bounds are also a little complicated:
\begin{equation} \int_{-1}^1 \int_0^{3-x} \ y^2\ \sqrt{\frac{1}{-x^2+1}}\ dy\ dx \end{equation}Great, we will now ask Sage to take the actual integral for us:
f(x,y) = y^2*sqrt(1/(-x^2+1)) f.integrate(y, 0, 3-x).integrate(x, -1,1)
Evidently, our result shows that the shape has a surface integral value of \(\frac{21\pi}{2} \approx 33\).
2 Jacobian Matrix
We will attempt to take the derivative matrix for this expression methodically.
Let's define the function as:
\begin{equation} f(x,y,z) = (z^2-\sin(y)) \hat{h} + (x+y+z) \hat{i} + (e^y +7x) \hat{j} + (ln(x+y-2z)) \hat{k} \end{equation}2.1 \(f_x\)
- \(f_x \cdot {\hat{h}} = 0\)
- \(f_x \cdot {\hat{i}} = 1\)
- \(f_x \cdot {\hat{j}} = 7\)
- \(f_x \cdot {\hat{k}} = \frac{1}{x+y-2z}\)
2.2 \(f_y\)
- \(f_y \cdot {\hat{h}} = -cos(y)\)
- \(f_y \cdot {\hat{i}} = 1\)
- \(f_y \cdot {\hat{j}} = e^y\)
- \(f_y \cdot {\hat{k}} = \frac{1}{x+y-2z}\)
2.3 \(f_z\)
- \(f_z \cdot {\hat{h}} = 0\)
- \(f_z \cdot {\hat{i}} = 1\)
- \(f_z \cdot {\hat{j}} = 0\)
- \(f_z \cdot {\hat{k}} = \frac{-2}{x+y-2z}\)
2.4 Jacobian
Finally, we can assemble the Jacobian matrix
\begin{equation} \nabla f = \begin{bmatrix} 0 & -\cos(y) & 0 \\ 1 & 1 & 1 \\ 7 & e^y & 0 \\ \frac{1}{x+y-2z} & \frac{1}{x+y-2z} & \frac{-2}{x+y-2z} \end{bmatrix} \end{equation}