Backlinks
We do the problems again, but corrected!
1 Single Value Function
\begin{align} &f_1: \mathbb{R}^2 \to \mathbb{R}^1 \\ &f_1(x,y) = 0 \end{align}What's the area of this function?
f(x,y) = 0 plot3d(f, (x,0,5), (y,0,7))
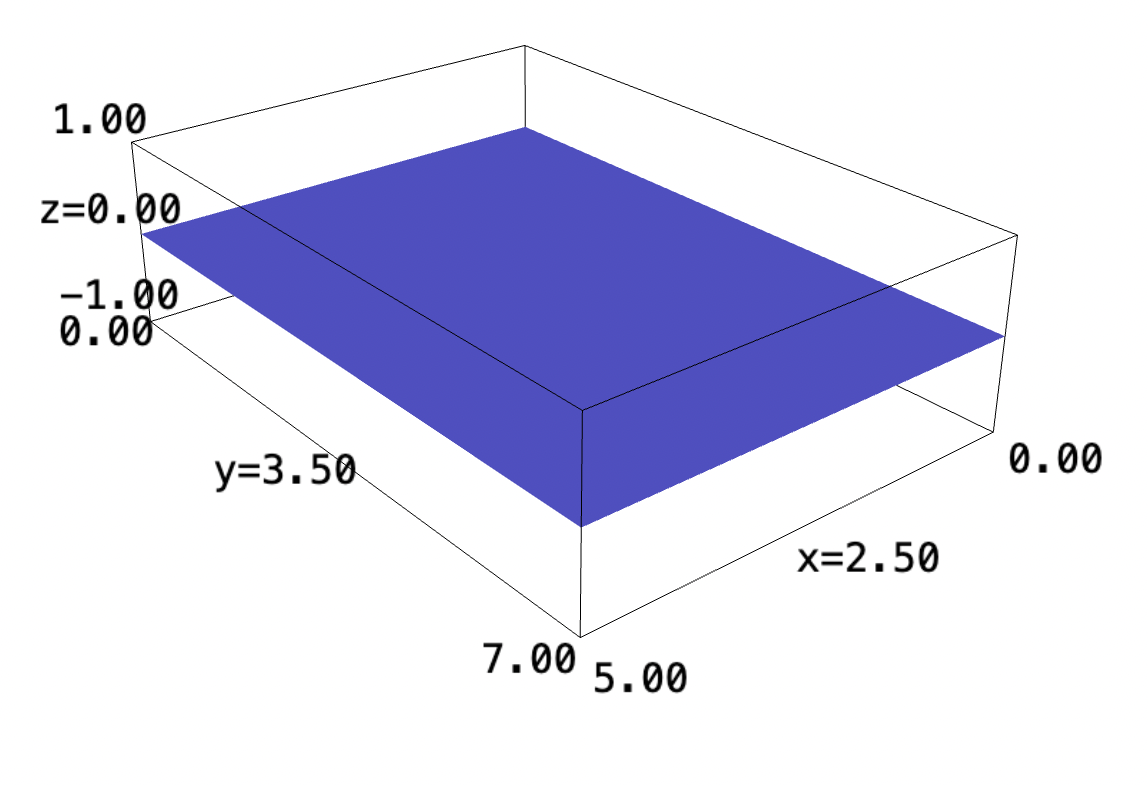
We can take the area of the shape, essentially by taking the volume by height \(1\): that is, for a rectangle of \(l,w,h\), its top-area is simply \(l\cdot w\), also known as \(lw\cdot 1\). Therefore:
\begin{equation} \int_0^7 \int_0^5 1 dx\ dy = 35 \end{equation}The area of the shape is therefore \(35\).
2 Area of the Plane
We want to first figure the correction per every given slice \(dA=n\ dV\) to setup a surface integral. By pythagoras (i.e. projecting the changes to the parallelity of the surface), we have that:
\begin{equation} dA = \sqrt{1+\left(\frac{\partial f}{\partial x}\right)^2+\left(\frac{\partial f}{\partial y}\right)^2}\ dV \end{equation}What's the area of the following function by \((5,7)\)?
\begin{align} &f_2: \mathbb{R}^2 \to \mathbb{R}^1 \\ &f_2(x,y) = 2x+3y+10 \end{align}
f(x,y) = 2*x+3*y+10 plot3d(f, (x,0,5), (y,0,7))
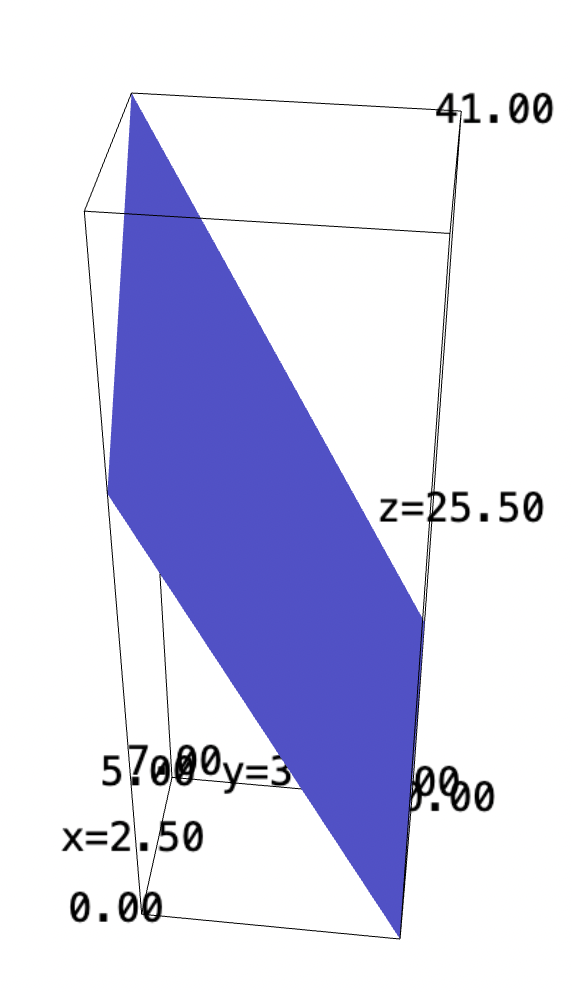
Therefore, taking the integral:
\begin{align} &\int_0^5 \int_0^7 \sqrt{14}\ dy\ dx \\ \Rightarrow & 35\sqrt{14} \end{align}float(35*sqrt(14))
It appears that the surface area is about \(130.958\) units.
3 Area of a Parabola
What's the area of the following function by \((5,7)\)?
\begin{align} &f_3: \mathbb{R}^2 \to \mathbb{R}^1 \\ &f_3(x,y) = x^2 \end{align}
f(x,y) = x^2 plot3d(f, (x,0,5), (y,0,7))

We will again find the area correction factor:
\begin{equation} dA = \sqrt{1+4x^2}\ dV \end{equation}And therefore, taking the integral:
\begin{equation} \int_0^5 \int_0^7 \sqrt{1+4x^2}\ dy\ dx \end{equation}This problem is solvable by trig substitution followed by integration by parts. For now, however, we will leverage a calculator.
f(x,y) = sqrt(1+4*x^2) f.integrate(y, 0,7).integrate(x,0,5) float(f.integrate(y, 0,7).integrate(x,0,5))
Evidently, the surface area of the shape is about \(181.1197\) units.
4 Another Surface Area
What's the area of the following function by \((5,7)\)?
\begin{align} &f_3: \mathbb{R}^2 \to \mathbb{R}^1 \\ &f_3(x,y) = x^2-y^2 \end{align}
f(x,y) = (x^2-y^2)*sqrt(1+4*x^2+4*y^2) plot3d(f, (x,0,5), (y,0,7))
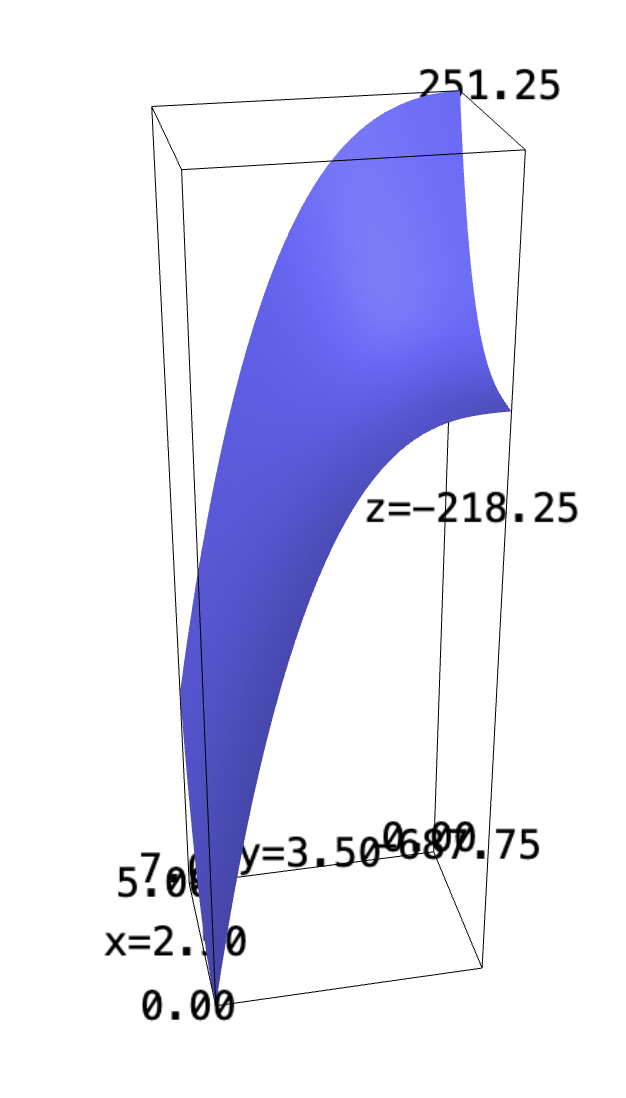
Let's instead parameterize this function first to take its surface area. We will take the most basic parameterization.
\begin{equation} \vec{v}(x,y) = x \hat{i} + y \hat{j} + (x^2-y^2) \hat{k} \end{equation}Taking, therefore, the partial derivatives:
\begin{align} &\frac{\partial \vec{v}}{\partial x} = \hat{i} + 2x \hat{k}\\ &\frac{\partial \vec{v}}{\partial y} = \hat{j} - 2y \hat{k} \end{align}Taking their cross product for the differential area, then:
\begin{align} & (\hat{i} + 2x \hat{k}) \times (\hat{j} - 2y \hat{k})\\ \Rightarrow & (\hat{i}\hat{j} + 2x \hat{k}\hat{j} - \hat{i}2y \hat{k} -2x \hat{k}2y \hat{k})\\ \Rightarrow & (\hat{k} - 2x \hat{i} + 2y \hat{j}) \end{align}We will take now the magnitude of this expression:
\begin{equation} \sqrt{1^2 + (-2x)^2 + (2y) ^2 } = \sqrt{1 + 4x^2 + 4y^2} \end{equation}We will again take this integral, digitally this time:
\begin{equation} \int_0^5 \int_0^7 \sqrt{1+4x^2+4y^2} \ dy\ dx \end{equation}f(x,y) = sqrt(1+4*x^2+4*y^2) f.integrate(y, 0,7).integrate(x,0,5) float(f.integrate(y, 0,7).integrate(x,0,5))
The shape is largely underneath the x-axis during the area on the rectangle. Therefore, we have an negative area! It is about \(326.55\) units.