Backlinks
1 Why be a king, when you can be a God?
We are going to take a definite integral across all of infinity by three dimensions.
\begin{equation} e(x,y,z) = \frac{1}{7^{(x^2+y^2+z^2)^{\frac{3}{2}}}} \end{equation}Given that universes are spheres and its far easier to take the spherical units here, we will take this integral with spherical coordinates.
We realize that \(x^2+y^2+z^2 = {\rho}^2\) in spherical space by pythagoras. Hence:
\begin{align} e(\rho, \theta, \phi) &= \frac{1}{7^{\rho^2^{\frac{3}{2}}}} \\ &= \frac{1}{7^{\rho^3}} \end{align}We note that, to calculate \(dV\), we have \(dV = \rho^2\ sin\theta\ d\phi\ d\theta\ d\rho\).
Taking the actual \(dV\), then:
\begin{equation} \iiint_V \frac{\rho^2\ \sin\theta}{7^{\rho^3}} \ d\phi\ d\theta\ d\rho \end{equation}Evidently, its time for \(u\) sub:
\begin{align} &u = \rho^3 \\ &\frac{du}{d\rho} = 3\rho^2 \\ &du = 3\rho^2\ d\rho \end{align}And hence:
\begin{equation} \iiint_V \frac{\sin\theta}{7^{u}} \ d\phi\ d\theta\ du \end{equation}We will take bounds by \([0, \pi]\), first against \(\phi\):
\begin{align} &\int_0^\pi \frac{\sin\theta}{7^{u}} \ d\phi\\ \Rightarrow &\frac{\pi\sin\theta}{7^{u}} \end{align}Great, we will now take the integral by \(\theta\), again by bounds \([0,\pi]\):
\begin{align} &\int_0^\pi \frac{\sin\theta}{7^{u}} \ d\theta\\ \Rightarrow &\frac{-\pi\cos\pi}{7^{u}} \\ \Rightarrow &\frac{\pi}{7^{u}} \end{align}And finally, we take the integral \(du\) from infinity:
\begin{align} &\int_0^\infty \frac{\pi}{7^{u}}\ du\\ \Rightarrow & \pi\int_0^\infty \frac{1}{7^{u}}\ du\\ \Rightarrow & \pi\int_0^\infty {7^{-u}}\ du\\ \Rightarrow & \left-\pi\ \frac{1}{7^x\ ln(7)}\right|_0^\infty \\ \Rightarrow & \frac{\pi}{ln(7)} \end{align}Multiplying the spherical result by \(2\) (we got half the circle), we get that the final energy is:
\begin{equation} \frac{2\pi}{ln(7)} \end{equation}The actual universe has net energy of \(0\) because its an infinitely large system with no external energy sources (as far as we know).
2 Area of a Circle
We can essentially leverage the polar expression:
\begin{equation} \iint_A \ dA \end{equation}In practice, this looks like:
\begin{align} &\int_0^r \int_0^{2\pi} r\ d\theta\ dr\\ \Rightarrow &\int_0^r 2\pi r\ dr\\ \Rightarrow & 2\pi \frac{r^2}{2}\\ \Rightarrow & \pi r^2\ \blacksquare \end{align}3 Sphere sticking out a cylinder
from sage.plot.plot3d.shapes import Sphere, Cylinder Sphere(1) + Cylinder(1/2, 2, color='red').translate(0,0,-1)
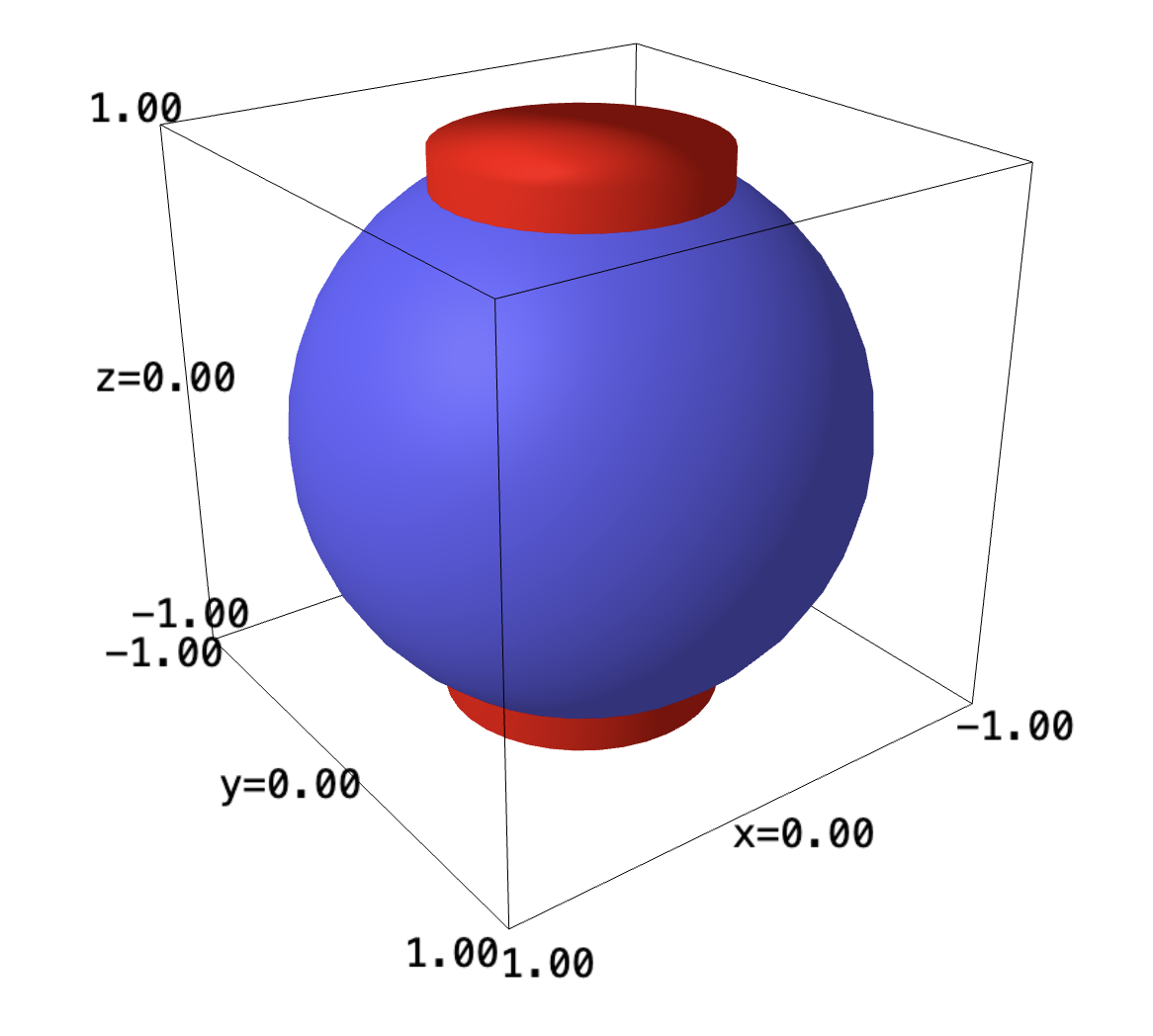
It looks like a little lantern!
We will first convert all of the system into a cylindrical system:
the sphere:
\begin{equation} r^2 + z^2 \leq 1 \end{equation}and, the cylinder:
\begin{equation} r = \frac{1}{2} \end{equation}We can see that our sphere is between \([-1,1]\) in all directions. Furthermore, our cylinder is cut in the middle.
For every slice, it contains an area of:
\begin{equation} \pi\ (r(h))^2\ dh \end{equation}where, \(r(h)\) is a function in \(h\) which maps the radius. We will note now that a large sphere is made of small concentric spheres. At every disk, a sphere's \(h\) (radius by height) would be the same as its \(r\) (radius by width).
Hence, we have:
\begin{equation} \pi h^2\ dh \end{equation}for every disk.
We furthermore have a tiny cut-out in the middle of the shape, of a cylinder of height \(dh\) and area \(\pi r^2 = \frac{\pi}{4}\).
For every disk, with the cut-out, then:
\begin{equation} \pi h^2\ dh - \frac{\pi}{4}\ dh \end{equation}We finally perform the integration:
\begin{align} &\int_{-1}^{1} \pi h^2\ dh - \frac{\pi}{4}\ dh\\ \Rightarrow\ &\left\left( \frac{h^3\pi}{3} - \frac{h\pi}{4}\right)\right|_{-1}^{1}\\ \Rightarrow\ &\frac{2\pi}{3} -\frac{2\pi}{4} \end{align}4 Volcano Volume
4.1 General volcano
To figure the volume of the shape \(f(x,y) = \frac{1}{(x^2+y^2)^k}\).
We will convert this system into polar form again for the ease of computation. Recall again that, by pythagoras, \(x^2+y^2 = r^2\).
Hence:
\begin{equation} f(r,\theta) = \frac{1}{r^{2k}} \end{equation}We will again take the integral, with ranges \(r=[0,1], \theta=[0,2\pi]\) from before, and \(dA=r\ dr\ d\theta\):
\begin{align} &\int_0^{2\pi} \int_0^1 r^{-k}\ dr\ d\theta\\ \Rightarrow &\int_0^{2\pi} \lim_{x\to 0} \left(\frac{1}{-k+1}-\frac{1}{x^{k-1}}\frac{1}{-k+1}\right)\ d\theta \end{align}Evidently, when \(k\leq 1\), the second term would become infinity large.
4.2 1D Volcano
We will take the same integral again, but in 1-d. We realize that \(\frac{1}{x}=ln(x)\), so, we have two cases:
Case 1: \(k \neq 1\)
\begin{align} &\int_{-1}^1 x^{-k} dx\\ \Rightarrow &\frac{1}{-k+1}-\frac{{-1}^{-k+1}}{-k+1} \end{align}where the value shifts between a real value for odd negative \(k\), and even for even negative \(k\).
Case 2: \(k=1\)
\begin{align} &\int_{-1}^1 x^{-1} dx\\ \Rightarrow &\left ln(x) \right|_{-1}^1 \end{align}Where, the second value would tend towards \(+\infty\).
Hence, when \(k=1\), the second term would become infinity large.