Backlinks
1 Two Dimensional Parabaloid, Problem 1
Consider a two-dimensional parabaloid:
\begin{equation} \begin{cases} f: \mathbb{R}^2 \to \mathbb{R}^1 \\ f(x,y) = x^2 + y^2 \end{cases} \end{equation}
f(x,y) = x^2 + y^2 plot3d(f, (x,-5,5),(y,-5,5))
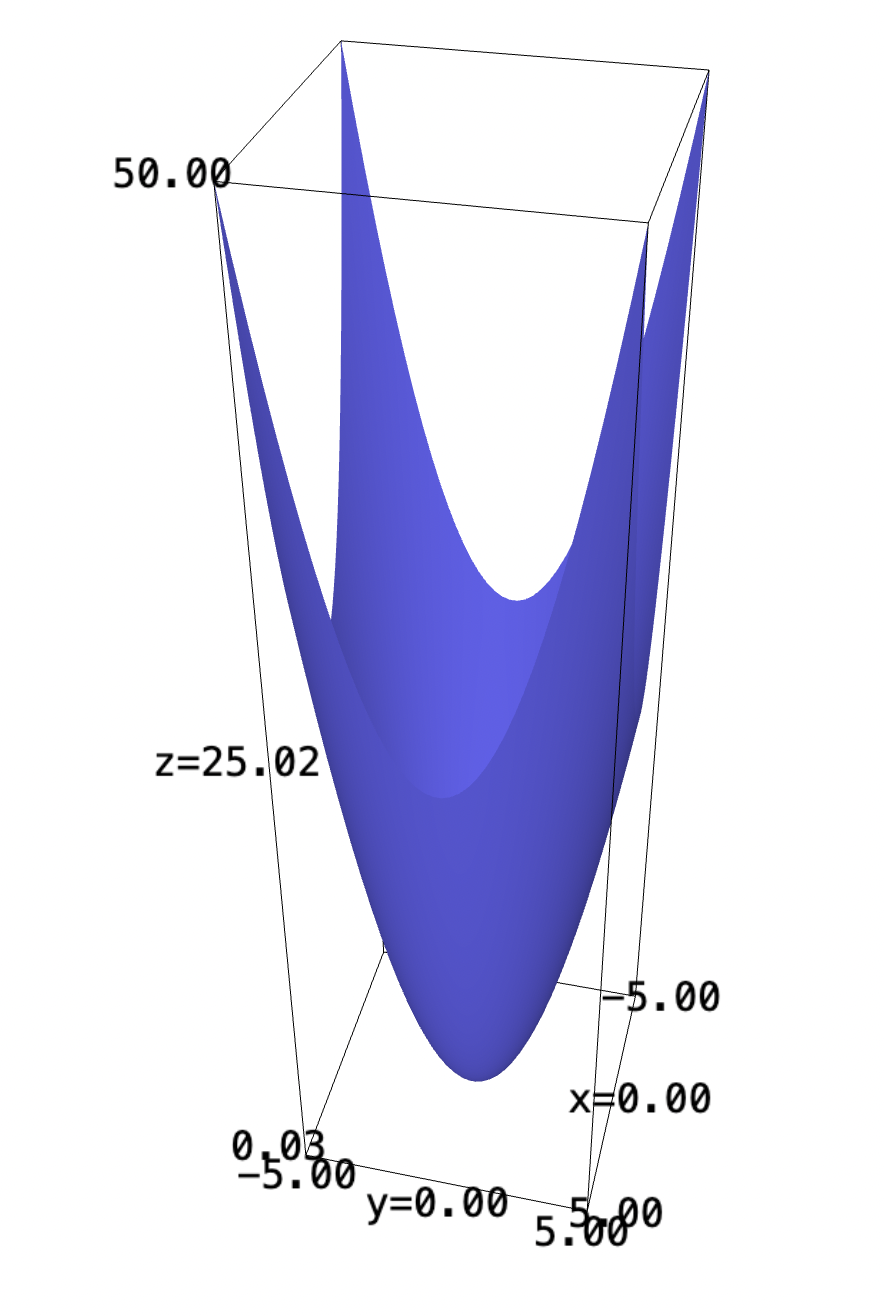
We will begin by writing a generalized parameterization of the expression.
For any given equation, we could take parameterization of:
\begin{equation} \begin{cases} y = sin(\theta)t + y_1 \\ x = cos(\theta)t + x_1 \end{cases} \end{equation}Supplying the values into the original expression:
\begin{equation} f(t) = (cos(\theta)t + x_1)^2 + (sin(\theta)t + y_1)^2 \end{equation}Expanding the square from before:
\begin{align} f(t) &= t^2cos(\theta)^2 + t^2sin(\theta)^2 + 2tx_1cos(\theta) + 2ty_1sin(\theta) + {x_1}^2 + {y_1}^2 \end{align}And finally, taking the derivative of the above expression:
\begin{equation} f'(t) = 2tcos(\theta)^2 + 2tsin(\theta)^2 + 2x_1cos(\theta) + 2y_1sin(\theta) \end{equation}For any given point, we will supply the \(0\) at that point as we are standing at that point:
\begin{equation} f'(x_1) = 2x_1cos(\theta) + 2y_1sin(\theta) \end{equation}
We now define a function f in sage which returns the parameterized derivative at any given point, given the point we are at and a \(\theta\), the angle we are facing.
f(x_1, y_1, theta) = 2*x_1*cos(theta) + 2*y_1*sin(theta) f
For the rest of the assignment, we could leverage this expression to figure the slope at a point.
1.1 Facing in a Direction
Suppose you are standing at the origin, facing \(+x\), how steep is the function?
- \(\theta=0\)
- \((x_1,y_1) = (0,0)\)
f(0,0,0)
At that function, the function is not steep at all. The slope is \(0\).
Suppose you are standing at \((0,12)\), facing \(+y\), how steep is the function?
- \(\theta=\frac{\pi}{2}\)
- \((x_1,y_1) = (0,12)\)
f(0,12,pi/2)
The slope is \(24\), at all locations where \({y_1}^2 = 24\).
Suppose you are standing at \((-3,0)\), facing \(-x\), how steep is the function?
- \(\theta = 0\)
- \((x_1,y_1) = (-3,0)\)
-f(-3, 0,0)
The function is a steepness of \(6\) units.
Suppose you are standing at \((7,7)\), facing in the direction of a \(45^{\circ}\) angle on the x-y plane, how steep is the function?
- \(\theta=\frac{\pi}{4}\)
- \((x_1,y_1) = (7,7)\)
float(f(7,7,pi/4))
The function is at a steepness of about \(19.8\) units.
Suppose you are standing at \((5,5\sqrt{3})\), facing in the \(+60^{\circ}\) direction on the x-y plane, how steep is the function?
- \(\theta = \frac{\pi}{3}\)
- \((x_1,y_1) = (5, 5\sqrt{3})\)
float(f(5,5*sqrt(3),pi/3))
The function is at a steepness of \(20\) units.
Suppose you are standing at \((5,5\sqrt{3})\), facing in the \(+45^{\circ}\) direction on the x-y plane, how steep is the function?
- \(\theta = \frac{\pi}{4}\)
- \((x_1,y_1) = (5, 5\sqrt{3})\)
float(f(5,5*sqrt(3),pi/4))
The function is at a steepness of \(19.32\) units.
Suppose you are standing at \((a,b)\), facing in the \(\theta\) direction on the x-y plane, how steep is the function?
As per the expression derived above, the steepness of the function at that point is:
\begin{equation} f'(x_1,y_1,\theta) = 2x_1cos(\theta) + 2y_1sin(\theta) \end{equation}Suppose you are standing at \((5,5\sqrt{3})\), when is the slope biggest?
The slope in the biggest in this example when, taken as the above function, there exists a critical point. This is also the same as when the function is turned in the direction of the gradient vector at that point. Namely:
\begin{equation} \begin{bmatrix} 2x \\ 2y \end{bmatrix} = \begin{bmatrix} 10 \\ 10\sqrt{3} \end{bmatrix} \end{equation}This corresponds to an angle of \(arctan(\sqrt{3}) \approx 1.04 rad\). It has a magnitude of \(30\) units.
If we turn for \(\frac{\pi}{2}\), we will find the angle orthogonal to the point, and which have the smallest slope of \(0\). If we turn for \(\pi\), we will find the angle with an equal steepness, but in the other direction, with a slope of \(-30\).
More generally: suppose you are standing on the function at some point, facing in some direction. What's the slope? What direction do you need to turn for it to be the flattest? What direction do you need to turn for it to be the steepest?
The slope of the function is found by the parameterized expression derived above, which would also be the dot product of the gradient against the direction vector. The steepest direction is the direction of the gradient, which is also the solution to critical points of the general parameterized expression w.r.t. \(\theta\). The flattest angle is the angle orthogonal to that angle, derived by \(\frac{\pi}{2}-\theta\).
2 Two Dimensional Parabaloid, Problem 1
Consider a two-dimensional parabaloid:
\begin{equation} \begin{cases} g: \mathbb{R}^2 \to \mathbb{R}^1 \\ f(x,y) = x^2 - y^2 \end{cases} \end{equation}
g(x,y) = x^2 - y^2 plot3d(g, (x,-5,5),(y,-5,5))
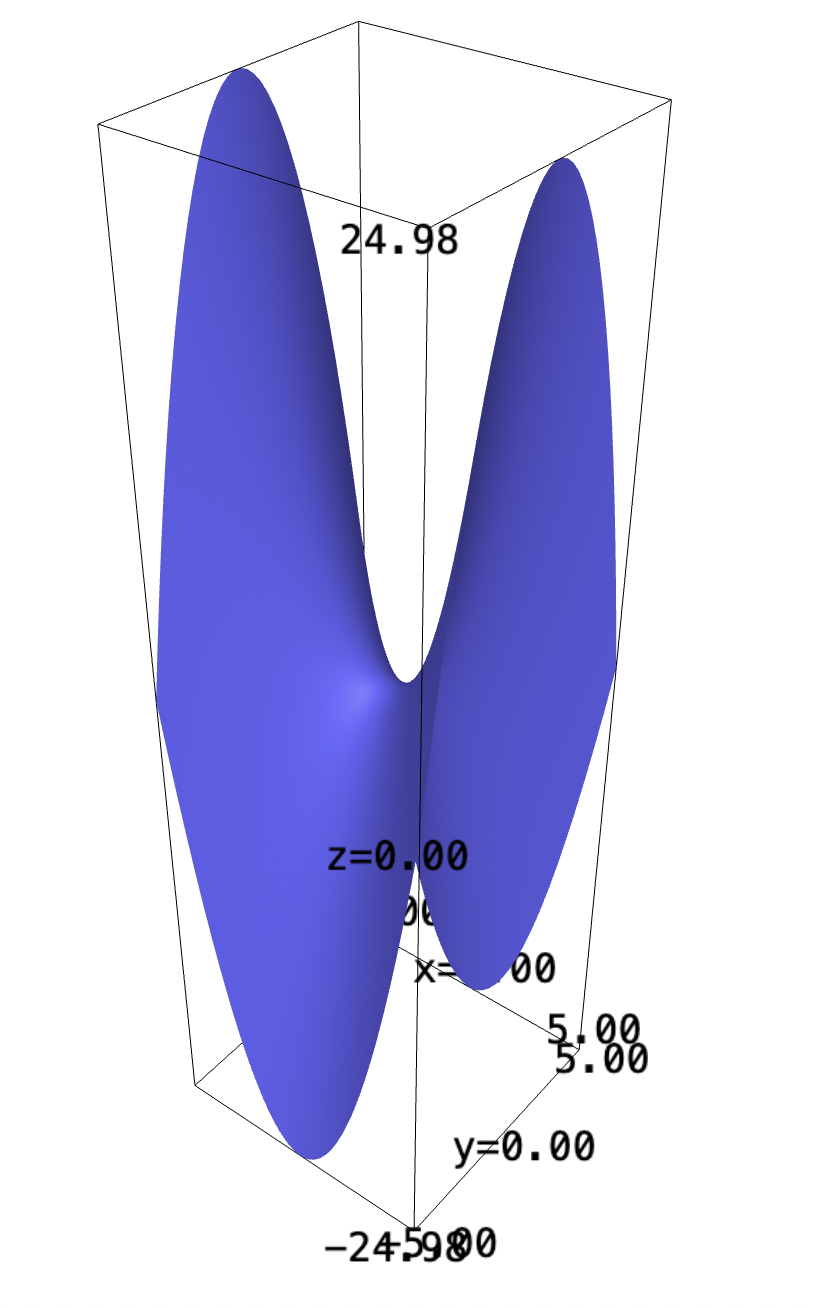
As with before, we will parameterize the expression along the following expressions:
\begin{equation} \begin{cases} y = sin(\theta)t + y_1 \\ x = cos(\theta)t + x_1 \end{cases} \end{equation}Supplying the values into the original expression:
\begin{equation} f(t) = (cos(\theta)t + x_1)^2 - (sin(\theta)t + y_1)^2 \end{equation}Expanding the square from before:
\begin{align} f(t) &= t^2cos(\theta)^2 - t^2sin(\theta)^2 + 2tx_1cos(\theta) - 2ty_1sin(\theta) + {x_1}^2 - {y_1}^2 \end{align}And finally, taking the derivative of the above expression:
\begin{equation} f'(t) = 2tcos(\theta)^2 - 2tsin(\theta)^2 + 2x_1cos(\theta) - 2y_1sin(\theta) \end{equation}For any given point, we will supply the \(0\) at that point as we are standing at that point:
\begin{equation} f'(x_1) = 2x_1cos(\theta) - 2y_1sin(\theta) \end{equation}
We now define a function g in sage which returns the parameterized derivative at any given point, given the point we are at and a \(\theta\), the angle we are facing.
g(x_1, y_1, theta) = 2*x_1*cos(theta) - 2*y_1*sin(theta) g
For the rest of the assignment, we could leverage this expression to figure the slope at a point.
2.1 Facing in a Direction
Suppose you are standing at the origin, facing \(+x\), how steep is the function?
- \(\theta=0\)
- \((x_1,y_1) = (0,0)\)
g(0,0,0)
At that function, the function is not steep at all. The slope is \(0\).
Suppose you are standing at \((0,12)\), facing \(+y\), how steep is the function?
- \(\theta=\frac{\pi}{2}\)
- \((x_1,y_1) = (0,12)\)
g(0,12,pi/2)
At that point, the slope is \(-24\).
Suppose you are standing at \((-3,0)\), facing \(-x\), how steep is the function?
- \(\theta = 0\)
- \((x_1,y_1) = (-3,0)\)
-g(-3, 0,0)
The function is a steepness of about \(6\) units.
Suppose you are standing at \((7,7)\), facing in the direction of a \(45^{\circ}\) angle on the x-y plane, how steep is the function?
- \(\theta=\frac{\pi}{4}\)
- \((x_1,y_1) = (7,7)\)
float(g(7,7,pi/4))
The function is at a steepness of \(0\) units.
Suppose you are standing at \((5,5\sqrt{3})\), facing in the \(+60^{\circ}\) direction on the x-y plane, how steep is the function?
- \(\theta = \frac{\pi}{3}\)
- \((x_1,y_1) = (5, 5\sqrt{3})\)
float(g(5,5*sqrt(3),pi/3))
The function is at a steepness of \(-10\) units.
Suppose you are standing at \((5,5\sqrt{3})\), facing in the \(+45^{\circ}\) direction on the x-y plane, how steep is the function?
- \(\theta = \frac{\pi}{4}\)
- \((x_1,y_1) = (5, 5\sqrt{4})\)
float(g(5,5*sqrt(3),pi/4))
The function is at a steepness of \(-5.18\) units.
Suppose you are standing at \((a,b)\), facing in the \(\theta\) direction on the x-y plane, how steep is the function?
As per the expression derived above, the steepness of the function at that point is:
\begin{equation} g'(x_1) = 2x_1cos(\theta) - 2y_1sin(\theta) \end{equation}Suppose you are standing at \((5,5\sqrt{3})\), when is the slope biggest?
The slope in the biggest in this example when, taken as the above function, there exists a critical point. This is also the same as when the function is turned in the direction of the gradient vector at that point. Namely:
\begin{equation} \begin{bmatrix} 2x \\ -2y \end{bmatrix} = \begin{bmatrix} 10 \\ -10\sqrt{3} \end{bmatrix} \end{equation}This corresponds to an angle of \(arctan(-\sqrt{3}) \approx -1.04 rad\). It has a magnitude of \(-30\) units. The slope of the function is found by the parameterized expression derived above, which would also be the dot product of the gradient against the direction vector. The steepest direction is the direction of the gradient, which is also the solution to critical points of the general parameterized expression w.r.t. \(\theta\). The flattest angle is the angle orthogonal to that angle, derived by \(\frac{\pi}{2}-\theta\).