Backlinks
You are building a swimming pool for outside of your Pringles-shaped house. It's going to be circular, with a \(40\) meter diameter. The depth will be constant latitudinally (i.e., along east-west lines), and will increase linearly from two meters at the south end to seven meters at the north end. How much water will you need to fill it? Calculate this both using a double integral a) in rectangular and b) in polar. How much will all that water cost? (Seriously! Look up whatever the prevailing water rates are in your municipality, or ask your parents about their water bill, and calculate it!) (Pictures!)
We know that the shape upon which are integrating would be circular, with radius \(20\). The shape of our pool would be latitudinally inclides along the north-south direction. If we define the latitudinal axis as \(x\), and the longitudinal ones as \(y\), we understand that the shape would be a function in \(y\).
At \(-20\), we will have a height of \(2\). At \(20\) (a whole diameter later), we will have a height of \(7\). Figuring the slope of this, we get that for a change in location by \(8\) units, we will have a change in height of \(1\) unit.
Supplying the expression into the slope of \(\frac{1}{8}\), to maintain \(y=-20\), and \(z=2\), we undrestand that the intercept ("bias") in the function would be \(4.5\).
Hence, the expression needed would be:
\begin{align} &f:\mathbb{R}^2 \to \mathbb{R}^1 \\ &f(x,y) = \frac{1}{8} y+4.5 \end{align}z = var("z")
def bound_fn(x,y,z):
return x^2 + y^2 < 20^2
f(x,y) = (1/8)*y+4.5
implicit_plot3d(f-z, (x, -20,20), (y, -20, 20), (z, 2,7), region=bound_fn, plot_points=100)
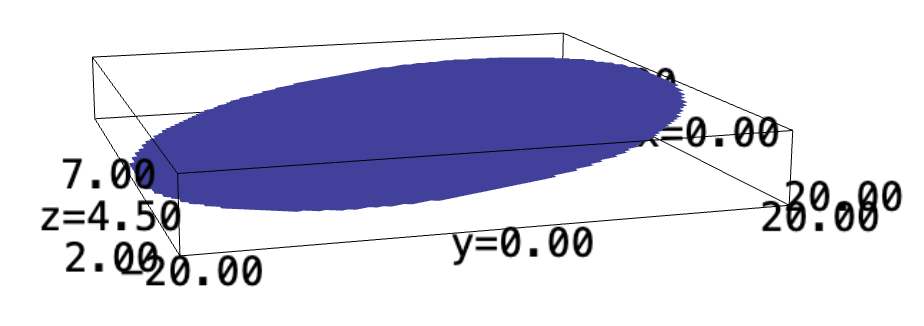
We will now take this expression in two ways: in both Cartesian and Cylindrical coordinates.
1 Cartesian Coordinates
Our function, expression again, would be:
\begin{equation} f(x,y) = \frac{1}{8}y + 4.5 \end{equation}Furthermore, our bound function can be expressed as:
\begin{equation} x^2+y^2 = 20^2 \end{equation}At every point \(x\), then, we can see that our bound renders it as \(y=\pm\sqrt{20^2-x^2}\) (the top and bottom half of circle). We will take this as our bound on \(y\) and integrate the function as such. We will integrate along the \(y\) dimension first, then integrate along \(x\).
\begin{align} &\int_{-20}^{20} \int_{-\sqrt{400-x^2}}^{\sqrt{400-x^2}} \frac{1}{8}y+4.5\ dy\ dx\\ \Rightarrow &\int_{-20}^{20} \left(\left\frac{1}{8} \frac{y^2}{2} + 4.5y \right|_{-\sqrt{400-x^2}}^{\sqrt{400-x^2}}\ \right) dx\\ \Rightarrow &\int_{-20}^{20} 9\sqrt{20^2-x^2}\ dx \end{align}At this point, we perform a trig substitution. We will substitute \(x = 20\sin\theta\), and therefore \(dx = 20\cos\theta d\theta\).
Performing the actual substitution, then:
\begin{align} &9\sqrt{20^2-20^2\sin^2 \theta}\ 20\cos\theta\ d\theta \\ \Rightarrow &9\sqrt{20^2(1-\sin^2 \theta)}\ 20\cos\theta\ d\theta \\ \Rightarrow &9\sqrt{20^2\cos^2\theta}\ 20\cos\theta\ d\theta \\ \Rightarrow &9(20^2\cos^2\theta) d\theta \\ \Rightarrow &3600\cos^2\theta d\theta \end{align}Let's further transform the bounds of the expression:
\begin{align} &20 = 20\sin \theta \\ \Rightarrow\ & 1 = \sin \theta \\ \Rightarrow\ & \theta = \frac{\pi}{2} \end{align} \begin{align} &-20 = 20\sin \theta \\ \Rightarrow\ & -1 = \sin \theta \\ \Rightarrow\ & \theta = \frac{3\pi}{2} \end{align}Supplying this back to the integral, we get that:
\begin{equation} \int_{\frac{\pi}{2}}^{\frac{3\pi}{2}} 3600\ cos^2 \theta d\theta \end{equation}We will transform this using the double-angle formula:
\begin{align} &\int_{\frac{\pi}{2}}^{\frac{3\pi}{2}} 3600\ cos^2 \theta d\theta\\ \Rightarrow & \int_{\frac{\pi}{2}}^{\frac{3\pi}{2}} 3600\ \frac{cos\ 2\theta + 1}{2} d\theta\\ \Rightarrow & \int_{\frac{\pi}{2}}^{\frac{3\pi}{2}} 1800\ (cos\ 2\theta + 1) d\theta\\ \Rightarrow & 1800\int_{\frac{\pi}{2}}^{\frac{3\pi}{2}} \ (cos\ 2\theta + 1) d\theta\\ \Rightarrow & 1800\left(\int_{\frac{\pi}{2}}^{\frac{3\pi}{2}} cos\ 2\theta\ d\theta+ \int_{\frac{\pi}{2}}^{\frac{3\pi}{2}} d\theta\right)\\ \Rightarrow & 1800\left(\frac{1}{2}\left sin\ 2\theta\ \right|_{\frac{\pi}{2}}^{\frac{3\pi}{2}}+ \pi\right)\\ \Rightarrow & 1800\pi \end{align}We can see that the area under this shape is \(1800\pi\).
2 Cylindrical Coordinates
Our function, at this point, is:
\begin{equation} f(x,y) = \frac{1}{8}y + 4.5 \end{equation}We will parameterize the function based on the regular parameterization scheme for polar/Cartesian conversion, based on triangles on the unit circle:
\begin{equation} \begin{cases} y = r\sin(\theta)\\ x = r\cos(\theta) \end{cases} \end{equation}Performing the actual parameterization, then:
\begin{equation} f(r, \theta) = \frac{1}{8}r\sin(\theta) + 4.5 \end{equation}We understand that, at area point \(d \theta\), the circumference of a ring upon which we are integrating is \(rd\theta\). Therefore:
\begin{equation} dA = r\ d\theta\ dr \end{equation}Taking the integral over a full circle with radius \(20\), then:
\begin{align} &\int_0^{20} \int_0^{2\pi} r\left(\frac{1}{8}r\sin(\theta) + 4.5\right) d\theta\ dr\\ \Rightarrow &\int_0^{20} \int_0^{2\pi} \left(\frac{1}{8}r^2\sin(\theta) + 4.5r\right) d\theta\ dr\\ \Rightarrow &\int_0^{20} \left \left(\frac{-1}{8}r^2\cos(\theta) + 4.5r\theta\right)\right|_0^{2\pi} \ dr\\ \Rightarrow &\int_0^{20} 9r\pi \ dr\\ \Rightarrow &\left \frac{9}{2}r^2\pi \right|_0^{20} \\ \Rightarrow &1800\pi \end{align}We can see that the value of the function under the circle is \(1800\pi\). This agrees with our previous derivation.
3 Filling the Tub with Things
We have a \(1800\pi\) tub. Let's fill it with things! For the sake of simplicity, we will set the units of the tub as litres. This means that the pool stores about \(5654.8\) litres of fluid.
As usual, Americans use absurd units. Performing the conversion by dividing by \(3.785\), this is about \(1493.86\) American liquid gallons.
3.1 Water
Taking the water flow change from the East Bay Municipal Water District for a single family dwelling not on a hill (so, discounting pressure surcharge), usages of \(172\) gallons per day costs \(4.42\), then from \(172\) to \(393\) gallon, it costs \(6.08\), finally from \(393\) gallons and above, it costs \(8.03\).
\(1493\) gallons is above all those limit values, it will cost our single family home \(8.03 \cdot 1493.68 = 11994.25\) dollars to fill the pool. That's enough money to buy this Used Honda Odyssey with 142k miles on it and enough money left over for a MacBook Pro.
3.2 Butter
For some reason, the idea of filling this pool with butter is endlessly entertaining to me. Turns out, the butters futures market does exist and is alive and well. As of today, the mean price of butter is \(6958\) per metric tonne. A litre of butter weighs about \(0.96\) kilograms. Hence, \(5654.8\) litres of butter is about \(5428.6\) kilos. This is about \(5.43\) tonnes.
Hence, it would cost \(37781.94\) to purchase enough butter to fill the pool. That's enough money to buy this very sad single-family home in Detroit, with enough money left over for title insurance and probably yet another MacBook Pro.
3.3 Oil
The price of oil is bleak these days in the US due to the Russo-Ukrainian war. Brent crude oil cost on average \(0.72\) per litre today. Hence, \(5654\) litres of crude oil, purchased today, would cost about \(4071.456\) dollars. It takes about \(158\) litres of crude oil (the weird constant is for a standard US barrel) to produce \(72\) litres of gasoline.
Hence, \(5654\) litres of gasoline produces about \(2576.87\) litres (\(680.73\) gallons) of gasoline. The used Honda Odyssey we brought just above has a gas milage of \(18\) MPG, which means the gasoline produced could run \(12253.14\) miles. Just enough to drive from SF to my hometown of Kunming in Southwestern China, then take a turn north and drive to Moscow to stop the war that got the oil prices so high in the first place.