Backlinks
1 Triple Osward's Box
To solve this problem, we will need to take a triple integral along each of the dimensions to add up the energy inside the box.
We know that the box is modeled by the function:
\begin{equation} e(x,y,z) = x^2y+11z+13 \end{equation}We further understand that one corner of the box is located at the origin and the other, at \((3,7,4)\).
We will now take the triple integral, one along each dimension:
\begin{equation} \int_0^4\ &\int_0^{7}\ \int_0^{3} x^2y+11z+13\ dx\ dy\ dz \end{equation}We will take parts of this integral at a time.
\begin{align} &\int_0^{3} x^2y+11z+13\ dx\\ =& \left \frac{x^3y}{3}+11zx+13x \right|_0^{3} \\ =& 9y+33z+39 \end{align}And now, we do this again for the second integral.
\begin{align} &\int_0^{7} 9y+33z+39 dy\\ =& \left \frac{9y^2}{2}+33zy+39y \right|_0^{7} \\ =& \frac{441}{2}+231z+273 \\ =& 493.5+231z \end{align}And finally, we take the third integral:
\begin{align} &\int_0^{4} 493.5+231z\ dz\\ =& \left 493.5z+\frac{231z^2}{2} \right|_0^{4} \\ =& 1974 + 1848 \\ =& 3822 \end{align}We can see there is \(3822\) total units of energy in the box.
2 Custom-Bound Integration
We are to find to volume beneath \(z=x^2\) via the bounds of \(xy=16\), \(y=x\), \(y=0\), and \(x=8\).
From the bound functions of \(y\), it is evident that the parameter \(y\) is bound by \([0,x]\). For the bounds of \(x\), we can figure that its bounded in the right by \(x=8\), and the right by \(x=\frac{16}{y}\).
Plotting the bounds together:
x,y = var("x y")
eqns = [y==0, y==x,x==8, x*y==16]
sum(implicit_plot(i, (x,0,16), (y,0,16)) for i in eqns)
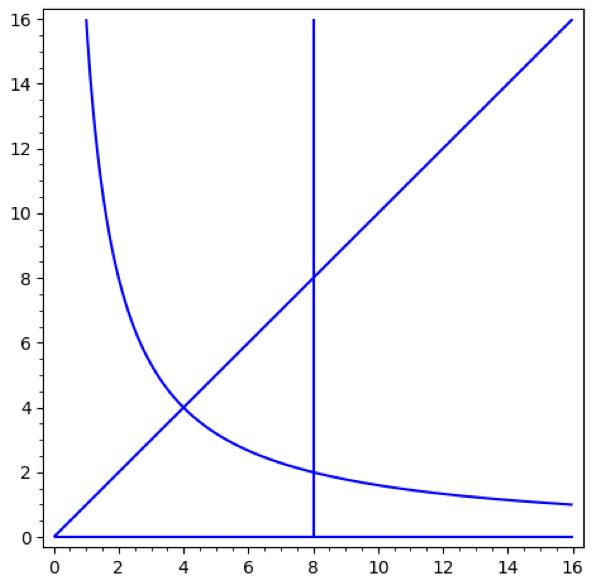
As per (not actually given) by the problem, we wish to find the "lower-left" region bound.
2.1 y-dimension first
Let's perform the integral along the \(y\) dimension first, reducing it to a function in \(x\).
We see that the top bound is by two piece-wise functions, each in one dimension of \(x\). We will perform the integral between bounds \([0,4]\).
\begin{align} &\int_0^x x^2 dy \\ \Rightarrow &x^3 \end{align}And, integrating between \([0,4]\), we have that:
\begin{align} &\int_0^4 x^3 dx \\ \Rightarrow & 64 \end{align}We find the integral now between \([4,8]\), with the bound:
\begin{align} &\int_0^{16/x} x^2 dy \\ \Rightarrow &\frac{16x^2}{x}\\ \Rightarrow &16x \end{align}And then, integrating along \([4,8]\):
\begin{align} &\int_4^8 16x dx \\ \Rightarrow & \left\frac{16x^2}{2} \right|_4^8 \\ \Rightarrow & 384 \end{align}The total area under the curve, then, is \(448\).
2.2 x-dimension first
We can do this again, but rotated. We can perform the integral along the \(x\) dimension, reducing it into a function in \(y\).
We see that the right is bound again by two piece-wise functions, each in one dimension of \(y\). We will perform the integral between the bounds \([0,2]\).
\begin{align} &\int_y^8 x^2 dx \\ \Rightarrow &\left \frac{x^3}{3}\right|_y^8\\ \Rightarrow &\left \frac{512}{3} - \frac{y^3}{3} \end{align}And then, we have to integrate between the bounds \([0,2]\).
\begin{align} &\int_0^2 \left(\frac{512}{3} - \frac{y^3}{3}\right)\ dy\\ \Rightarrow &\left\frac{512y}{3} - \frac{y^4}{12}\right|_0^2\ dy\\ \Rightarrow &\left\frac{1024}{3} - \frac{16}{12} \\ \Rightarrow &\left\frac{4080}{12} = 340 \end{align}We can perform the integration again \([2,4]\).
\begin{align} &\int_y^{16/y} x^2 dx \\ \Rightarrow &\left \frac{x^3}{3}\right|_y^{16/y}\\ \Rightarrow &\left \frac{4096}{3y^3} - \frac{y^3}{3}\\ \Rightarrow &\left \frac{4096y^{-3}}{3} - \frac{y^3}{3} \end{align}And then, we will integrate by the bounds \([2,4]\):
\begin{align} &\int_2^4 \frac{4096y^{-3}}{3} - \frac{y^3}{3}\ dy\\ \Rightarrow &\left\frac{4096y^{-2}}{-6} - \frac{y^4}{4}\right|_2^4\\ \Rightarrow &108 \end{align}Hence, the total area under the curve would also be \(448\) units.
As we can see, the two integrals agree with respect to the area in that corner.
3 Cylindrical Coordinates
To find the volume upon \(f(x,y) = 7+x+y\) above a circle of radius \(5\), we can leverage cylindrical coordinates.
x,y,z = var("x y z")
f(x,y) = 7+x+y
implicit_plot3d(7+x+y-z, (x,-10,10), (y,-10,10), (z,-10,10), region=lambda x,y,z:(x**2+y**2)<5, plot_points=200)
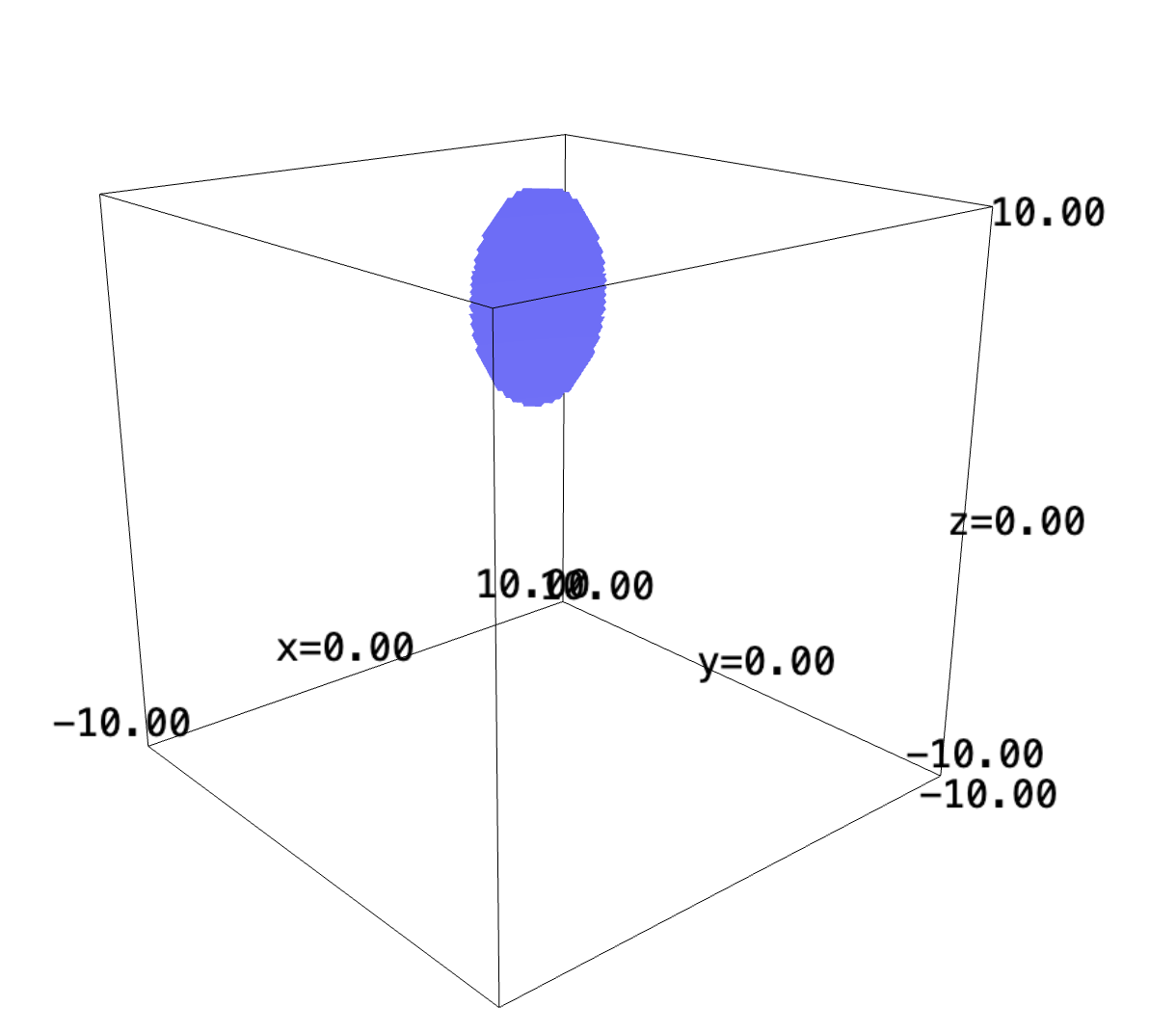
Recall that, given an unit circle, we have:
\begin{equation} \begin{cases} x = r\ cos(\theta)\\ y = r\ sin(\theta) \end{cases} \end{equation}Supplying the radius of \(5\) to the expression, we have the following parameterization:
\begin{equation} \begin{cases} x = 5\ cos(t)\\ y = 5\ sin(t) \end{cases} \end{equation}We can further figure the change of the function along \(t\). That is:
\begin{equation} \begin{cases} \frac{dx}{dt} = -5\ sin(t)\\ \frac{dy}{dt} = 5\ cos(t) \end{cases} \end{equation}And furthermore, we can see that \(\frac{df}{dt}\) is:
\begin{equation} \frac{df}{dt} = 5 \end{equation}To take the parameterization, we finally get that:
\begin{equation} f(t) = 7+5\ cos(t)+ 5\ sin(t) \end{equation}Finally the integral between \(0\) and \(2\pi\):
\begin{align} &\int_0^{2\pi} 5f(t)\ dt\\ \Rightarrow\ &\int_0^{2\pi} 5(7+5\ cos(t)+ 5\ sin(t))\ dt\\ \Rightarrow\ &\int_0^{2\pi} 35+25\ cos(t)+ 25\ sin(t)\ dt\\ \Rightarrow\ &\left 35t+25\ sin(t)- 25\ cos(t)\ \right|_0^{2\pi}\\ \Rightarrow\ &\left 70\pi- 25 \end{align}The line integral under the curve is \(70\pi-25\).