Backlinks
Table of Contents
Given:
\begin{equation} \begin{cases} f(x,y): \mathbb{R}^2 \to \mathbb{R}^1 \\ f(x,y) = sin(x)cos(y) +5 \end{cases} \end{equation}
f(x,y) = sin(x)*cos(y) +5 plot3d(f, (x,-5,5), (y,-5,5))
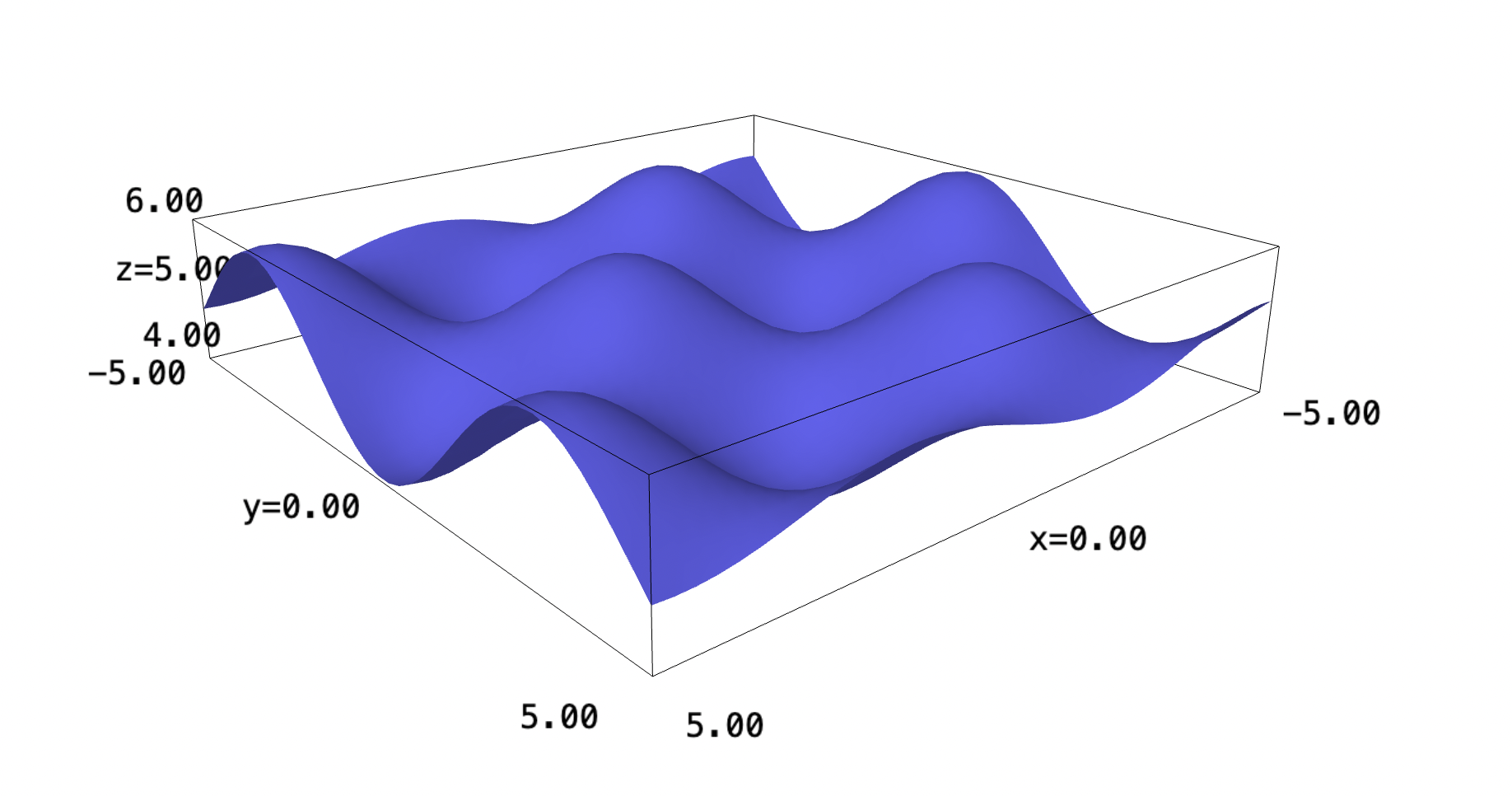
1 Problem 1
What is the integral of the function along
\begin{equation} y = 0, \{0 \leq x\leq 3\pi\} \end{equation}
We begin by the parameterization of the function, slicing along the bottom edge. We understand, therefore, that we are parameterize by:
\begin{equation} \begin{cases} x=t \\ y=0 \end{cases} \end{equation}\(t = 3\pi\) when \(x=3\pi\), meaning our bounds are \([0, 3\pi]\).
Performing the actual parameterization, then:
\begin{align} &f(t,0) = sin(t) \cdot 1 + 5 \\ &f(t) = sin(t) \cdot 1 + 5 \end{align}in units of \(t\). We then figure the correction to \(\frac{dy}{dx}\) for which it contributes. Every value of \(t\), along the curve, contributes \(\sqrt{\left(\frac{dx}{dt}\right)^2 + \left(\frac{dy}{dt}\right)^2}\) of distance. We see from the above parameterization, that:
\begin{equation} \begin{cases} \frac{dx}{dt} = 1\\ \frac{dy}{dt} = 0\\ \end{cases} \end{equation}Therefore:
\begin{equation} \sqrt{\left(\frac{dx}{dt}\right)^2 + \left(\frac{dy}{dt}\right)^2} = 1 \end{equation}And finally, taking the integral:
\begin{align} \int^{3\pi}_0 (sin(t) +5) \cdot 1\ dt &= (-cos(t) + 5t) |^{3\pi}_0\\ &= (1+15 \pi) - (-1) \\ &= 15 \pi +2 \end{align}2 Problem 2
What is the integral of the function along
\begin{equation} y = x, \{0 \leq x\leq 3\pi\}, \{0 \leq y\leq 3\pi\} \end{equation}
We begin by the parameterization of the function, slicing along the bottom edge. We understand, therefore, that we are parameterize by:
\begin{equation} \begin{cases} x=t \\ y=t \end{cases} \end{equation}\(t = 3\pi\) when \(y=x=3\pi\), meaning our bounds are \([0, 3\pi]\).
Performing the actual parameterization, then:
\begin{align} &f(t,t) = sin(t) cos(t) + 5 \\ &f(t,t) = \frac{1}{2} (2sin(t)cos(t)) + 5 \\ &f(t) = \frac{1}{2} sin(2t) + 5 \end{align}in units of \(t\). We then figure the correction to \(\frac{dy}{dx}\) for which it contributes. Every value of \(t\), along the curve, contributes \(\sqrt{\left(\frac{dx}{dt}\right)^2 + \left(\frac{dy}{dt}\right)^2}\) of distance. We see from the above parameterization, that:
\begin{equation} \begin{cases} \frac{dx}{dt} = 1\\ \frac{dy}{dt} = 1\\ \end{cases} \end{equation}Therefore:
\begin{equation} \sqrt{\left(\frac{dx}{dt}\right)^2 + \left(\frac{dy}{dt}\right)^2} = \sqrt{2} \end{equation}And finally, taking the integral:
\begin{align} &\int^{3\pi}_0 \left(\frac{1}{2}sin(2t) +5\right)\cdot \sqrt{2} \ dt \\ &= \int^{3\pi}_0 \frac{1}{2}sin(2t)\sqrt{2} dt+\int^{3\pi}_05\sqrt{2} \ dt \\ &= \left\left(\frac{-1}{4}cos(2t)\sqrt{2}\right)\right|^{3\pi}_0 + 5t\sqrt{2}\rvert^{3\pi}_0\\ &= 15\pi \sqrt{2} \end{align}3 Problem 3
What is the integral of the function along
\begin{equation} y = x^2, \{0 \leq x\leq 2\pi\}, \{0 \leq y\leq 4\pi^2\pi\} \end{equation}
We begin by the parameterization of the function, slicing along the bottom edge. We understand, therefore, that we are parameterize by:
\begin{equation} \begin{cases} x=t \\ y=t^2 \end{cases} \end{equation}\(t = 2\pi\) when \(y=4\pi^2, x=2\pi\), meaning our bounds are \([0, 2\pi]\).
Performing the actual parameterization, then:
\begin{align} &f(t,t^2) = sin(t)cos(t^2)+5\\ &f(t) = sin(t)cos(t^2)+5 \end{align}in units of \(t\). We then figure the correction to \(\frac{dy}{dx}\) for which it contributes. Every value of \(t\), along the curve, contributes \(\sqrt{\left(\frac{dx}{dt}\right)^2 + \left(\frac{dy}{dt}\right)^2}\) of distance. We see from the above parameterization, that:
\begin{equation} \begin{cases} \frac{dx}{dt} = 1\\ \frac{dy}{dt} = 2t\\ \end{cases} \end{equation}Therefore:
\begin{equation} \sqrt{\left(\frac{dx}{dt}\right)^2 + \left(\frac{dy}{dt}\right)^2} = \sqrt{1+4t^2} \end{equation}And finally, taking the integral:
\begin{align} &\int^{2\pi}_0 \left(\frac{1}{2}sin(2t) +5\right)\cdot \sqrt{1+4t^2} \ dt \end{align}We will now solve this integral analytically:
t = var("t")
definite_integral((0.5*sin(2*t)+5)*sqrt(1+4*t^2), t, 0, 2*pi)
It appears that the area under the parameterized curve is about 199 units.