Table of Contents
There is brief discussion in the DGC book with respect to cylindrical coordinates; let's define a system oriented along the following figure given by the book:
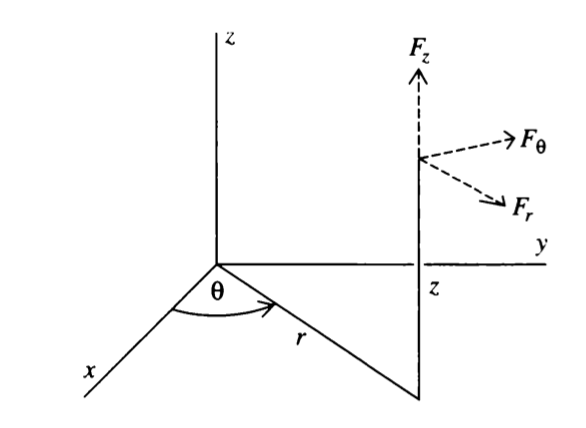
1 Cylindrical coordinates
let's return to our originally expression for a surface integral with respect to some surface with normal \(\hat{n}\).
\begin{equation} \iint_S \vec{F} \cdot \hat{n}\ dS \end{equation}Let's figure out the surface integral of a "cylindrical cuboid" (spinning a cube around \(z\)) on this plane!
We will define the center of the cube to be at \((r, \theta, z)\), and its "width" to be at some infinitesimal \(\Delta r\). Therefore, the "front" (curved) face is located at, sweeping across \(\theta\) and \(z\):
\begin{equation} \left(r + \frac{\Delta r}{2}, \theta, z\right) \end{equation}We will be calculating flux that travels across this surface. The "material" that we need to push through would be:
\begin{equation} \left(r+ \frac{\Delta r}{2}\right) \end{equation}Additionally, the cross-sectional value function at that surface would be the \(r\) component of our value function \(\vec{F}\): \(\vec{F_r}\). Hence, the flux expression is:
\begin{equation} \iint_{S_1} F_r\left(r + \frac{\Delta r}{2}, \theta, z\right) \left(r+ \frac{\Delta r}{2}\right) \Delta \theta \Delta z \end{equation}The opposite direction ("inside" the cylinder), is simply the negative of the value function and direction (i.e. adding \(\Delta r\) in the opposite direction).
\begin{equation} \iint_{S_2} -F_r\left(r - \frac{\Delta r}{2}, \theta, z\right) \left(r- \frac{\Delta r}{2}\right) \Delta \theta \Delta z \end{equation}In total, the expression of the two values added would be:
\begin{equation} F_r\left(r + \frac{\Delta r}{2}, \theta, z\right) \left(r+ \frac{\Delta r}{2}\right) \Delta \theta \Delta z-F_r\left(r - \frac{\Delta r}{2}, \theta, z\right) \left(r- \frac{\Delta r}{2}\right) \Delta \theta \Delta z \end{equation}Finally, to calculate the desired divergence at that point, we will divide the resulted by \(\frac{1}{\Delta V} = \frac{1}{\Delta \theta \Delta z r\Delta r}\)
Therefore, the expression becomes:
\begin{equation} \frac{1}{r\Delta r} \left[F_r\left(r + \frac{\Delta r}{2}, \theta, z\right) \left(r+ \frac{\Delta r}{2}\right) -F_r\left(r - \frac{\Delta r}{2}, \theta, z\right) \left(r- \frac{\Delta r}{2}\right) \right] \end{equation}Lastly, we will take the limit as \(\Delta r\) (i.e. \(\Delta V\)) approaches zero. We will do this in three steps:
First, we will factor out the \(\frac{1}{r}\) component:
\begin{align} &\frac{1}{r \Delta r} \left[F_r\left(r + \frac{\Delta r}{2}, \theta, z\right) \left(r+ \frac{\Delta r}{2}\right) -F_r\left(r - \frac{\Delta r}{2}, \theta, z\right) \left(r- \frac{\Delta r}{2}\right) \right]\\ \Rightarrow &\ \frac{1}{r} \frac{\left[F_r\left(r + \frac{\Delta r}{2}, \theta, z\right)r - F_r\left(r - \frac{\Delta r}{2}, \theta, z\right)r \right]}{\Delta r} \\ \Rightarrow &\ \frac{1}{r} \frac{\partial}{\partial r} (rF_r) \end{align}Expanding over each dimension, therefore:
\begin{equation} div\ \vec{F} = \frac{1}{r}\frac{\partial}{\partial r}(rF_r) + \frac{1}{r}\frac{\partial F_{\theta}}{\partial \theta} + \frac{\partial F_{z}}{\partial z} \end{equation}And hence, divergence in cylindrical coordinates work in exactly the same way as that in rectangular ones.
2 Spherical Coordinates
We will apply a similar reasoning to prove the flux/divergence in spherical coordinates. Most of the content here is functionally equivalent.
We will first create the conception of a "spherical cuboid". It is essentially the same idea as the cylindrical cuboid, but the flat edge is now curved downwards to become a sectional sphere.
The front edge and back edges can be modeled very similarly as before. Except the \(r\pm\frac{\Delta r}{2}\) terms are squared in order to accommodate for the new \(\Delta \theta\) and \(\Delta \phi\) terms (i.e. we need to find "circumference" on both.
The proposed center is still at its original position, that:
\begin{equation} \left(r+\frac{r}{2},\theta,\phi\right) \end{equation}The logic carries from before of the same calculation of flux: the value function along the \(r\) direction, multiplied by the area of the surface cross-section. The logic would be almost exactly the same, except the "radius" section is squared as there are two angles for which the "circumference" that makes up the area of cross-section is calculated.
In total, the expression of the two values added would be:
\begin{equation} F_r\left(r + \frac{\Delta r}{2}, \theta, z\right) \left(r+ \frac{\Delta r}{2}\right)^2 \Delta \theta \Delta \phi-F_r\left(r - \frac{\Delta r}{2}, \theta, z\right) \left(r- \frac{\Delta r}{2}\right)^2 \Delta \theta \Delta \phi \end{equation}Dividing the expression by \(\Delta V\) and taking the limit, as with the definition from before, then:
\begin{align} &\frac{F_r\left(r + \frac{\Delta r}{2}, \theta, z\right) \left(r+ \frac{\Delta r}{2}\right)^2 -F_r\left(r - \frac{\Delta r}{2}, \theta, z\right) \left(r- \frac{\Delta r}{2}\right)^2}{r \Delta r} \\ \Rightarrow &\frac{1}{r} \frac{F_r\left(r + \frac{\Delta r}{2}, \theta, z\right) \left(r+ \frac{\Delta r}{2}\right)^2 -F_r\left(r - \frac{\Delta r}{2}, \theta, z\right) \left(r- \frac{\Delta r}{2}\right)^2}{\Delta r} \\ \end{align}We will finally take the limit as \(\Delta r \to 0\), applying the same logic as before that the expression forms the formal definition of a derivative \(\frac{\partial F_r}{\partial r}\) multiplied by \(r\) (as \(\frac{\Delta r}{2} = 0\)) twice. Therefore, the final expression in the \(r\) direction is:
\begin{equation} \frac{1}{r^2}\frac{\partial}{\partial r} (r^2F_f) \end{equation}The same logic follows for all other directions, though the area for \(r\) value is replaced by \(\sin{\{\theta,\phi\}}\) as we are looking for a length and not an angle.
The final expression, therefore, for spherical coordinates:
\begin{equation} \frac{1}{r^2}\frac{\partial}{\partial r} (r^2F_f) + \frac{1}{r\sin{\phi}}\frac{\partial}{\partial \phi}(\sin \phiF_{\phi}) \end{equation}