Backlinks
#ret
1 Square roots of \(i\)
20math530retSquareRootsi.pdf Didn't figure it out. How did I get \(a = \pm\frac{\sqrt{2}i}{2}\)??
2 Cross product
Find the cross product of \(\begin{pmatrix}1\\3\\0\end{pmatrix}\times\begin{pmatrix}2\\2\\-1\end{pmatrix}\)
\[
\begin{split} \Rightarrow&\left|\begin{matrix}i&j&k\\1&3&0\\2&2&-1\end{matrix}\right|\\ \Rightarrow&i\left|\begin{matrix}3&0\\2&-1\end{matrix}\right| +j\left|\begin{matrix}0&1\\-1&2\end{matrix}\right| +k\left|\begin{matrix}1&3\\2&2\end{matrix}\right|\\ \Rightarrow& -3i + 1j -4k\\ \Rightarrow& \begin{bmatrix}-3\\1\\-4\end{bmatrix} \end{split}\]
3 Read Chapter 1.B
3.1 Vector Space Addition/scalarmult
- Every pair of elements is in \(V\) can be added together to form another element in \(V\) (closed)
- A scalar is anything in \(F\), which means it might be complex! ### Vector space definition
- communativity(!): \(u +v = v+u. \forall u, v \in V\)
- associativity: \((u+v)+w = u+(v+w) and (ab)v = a(bv). \forall u, v, w \in V. \forall a, b \in F\)
- additive identity: \(\exists 0\in V \mid v + 0 = v. \forall v \in V\)
- Additive inverse
- Multiplicative identity (denoted \(1\))
- distributive property (both front and back) A vector space depneds on \(F\) so \(V\) is a vector space over \(F\) ### Vector spaces with other sets? \(F^S\)
- \(F^S\) is the set of functions from \(S\) to \(F\)
- meaning that it's all functions whose domains are subsets of \(S\) and ranges are subsets of \(F\)?
- addition \(f, g \in F^S, x \in F: (f + g)(x) = f(x)+g(x)\)
- multiplication: \(\lambda \in F\) and \(f \in F^S : \lambda F \in F^S = (\lambda f)(x) = \lambda f(x)\)
- functions can be elements in fields or something?
- lists are just functions on a set of numbers..?
- subtraction (additive inverses and identity are unique)
When you see \(xy\), one of them has to be a vector because there is no scalar scalar multiplication defined ## Show that \(a\bullet b = |a||b|cos\theta\) Suppose \(a = \begin{bmatrix}x\\y\end{bmatrix}\) and \(b = \begin{bmatrix}w\\z\end{bmatrix}\). We have \(a\bullet b = a^T\cdot b = \begin{bmatrix}x&y\end{bmatrix} \begin{bmatrix}w\\z\end{bmatrix} = xw+yz\). We need an expresion for \(\theta\):
\begin{split} |A||B|cos\theta &= |A||B| cos\left(\frac{\pi}{2}-\alpha-\beta\right)\\ &= |A||B| sin(\alpha + \beta)\\ &= |A||B| \left(sin\alpha\ cos\beta + cos\alpha\ sin\beta\right)\\ &= |A||B| \left(\left(\frac{y}{|A|}\right)\left(\frac{z}{|B|}\right)+\left(\frac{x}{|A|}\right)\left(\frac{w}{|B|}\right)\right)\\ &= |A||B| \left(\frac{yz}{|A||B|}+\frac{xw}{|A||B|}\right)\\ &= yz+wz\\ &= xw+yz \end{split}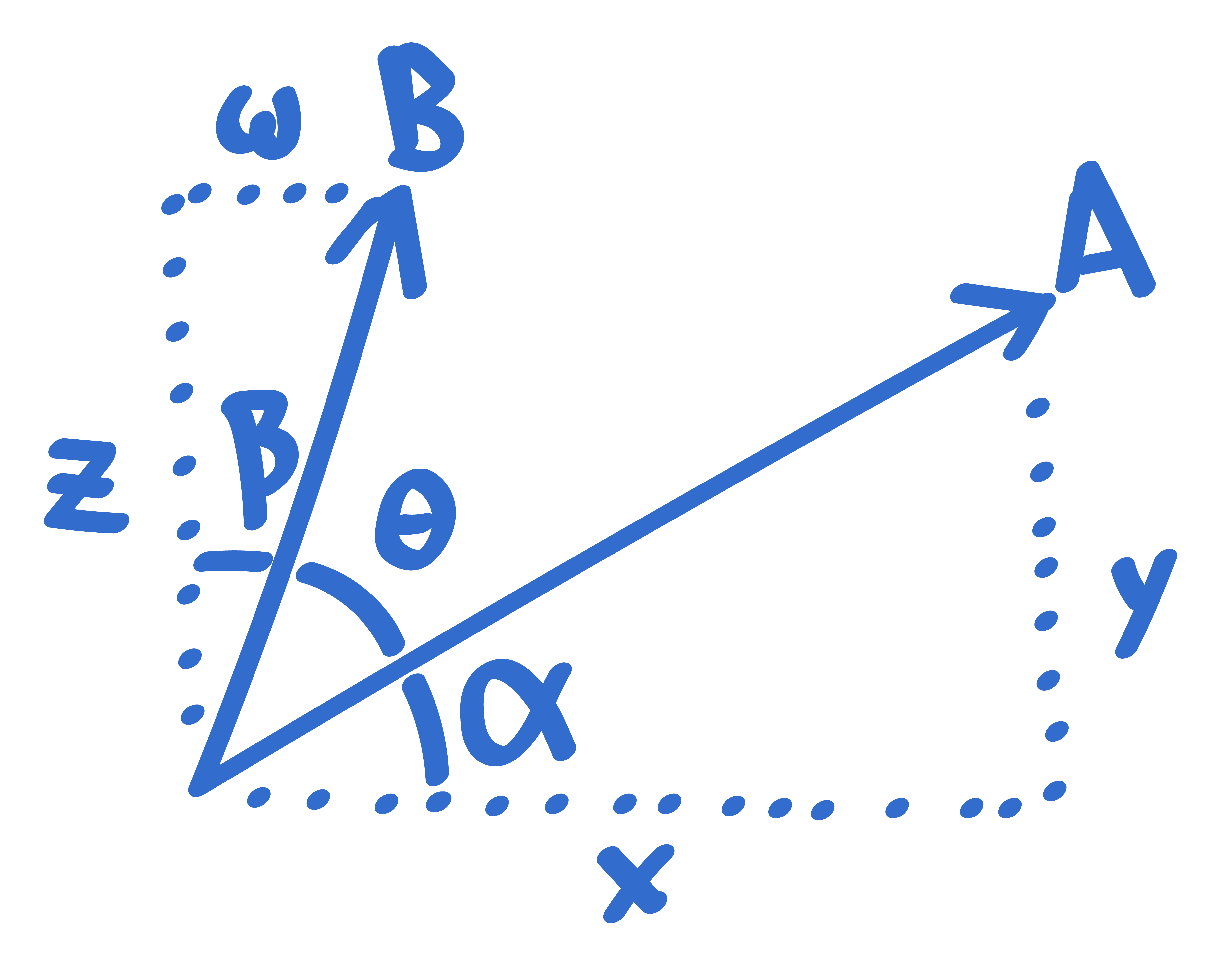
As seen in the diagram,
\(\theta = \frac{\pi}{2} - \alpha - \beta\). Finally: \[
\]
4 Epilogue
That was two hours… I'll save the proving integers mod 3 are a field for later. #todo-exr0n